SVM

선형, 비선형 분류, 회귀, 이상치 탐색에 사용할 수 있는 다목적 머신러닝 모델이다.

•

복잡한 분류 문제에 잘 들어맞는다.

•

중간 크기의 데이터셋에 적합하다. 

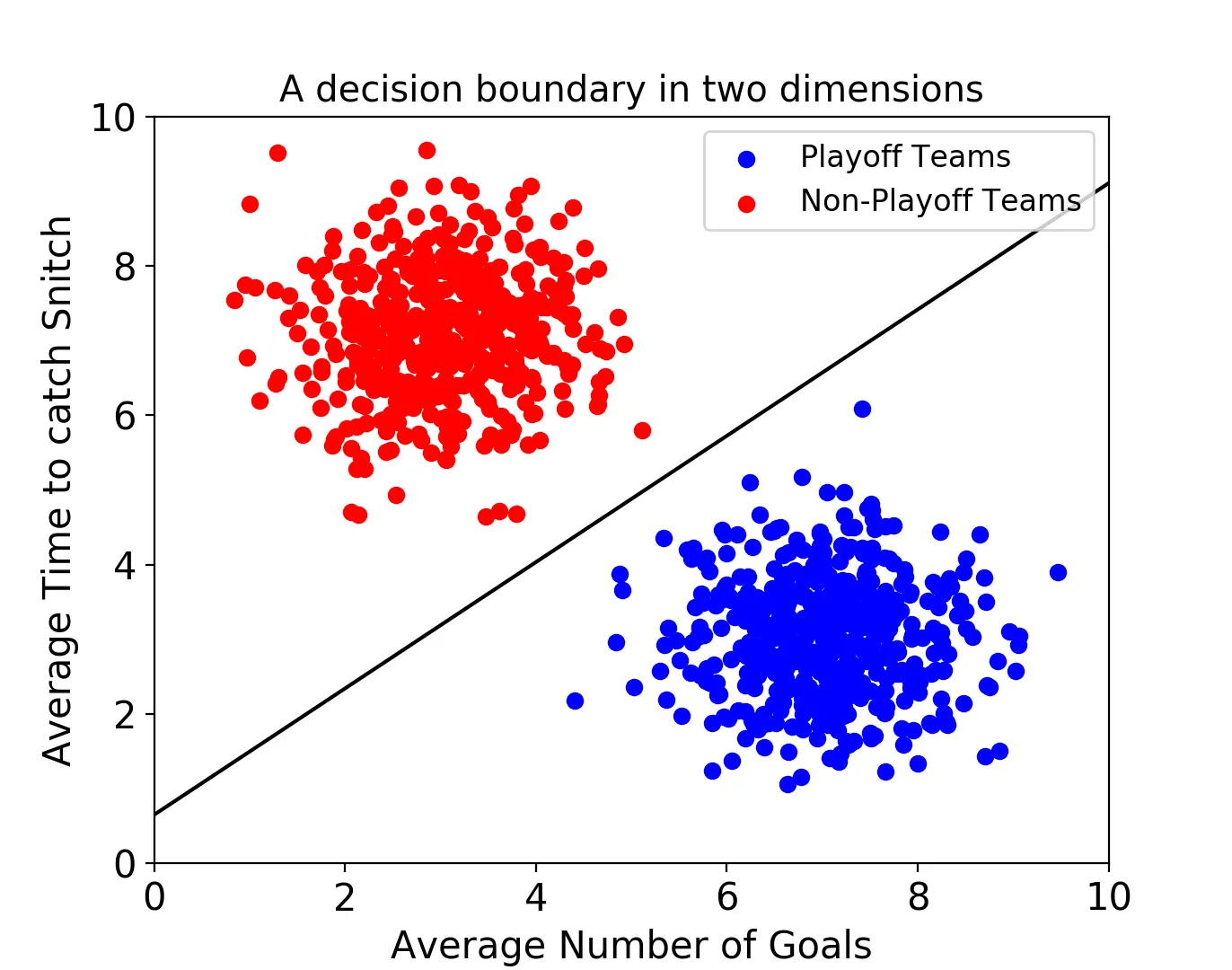
서포트 벡터 머신은 결정 경계(Decision Boundary) , 즉 분류를 위한 기준 선을 정의하는 모델이다.

만약, 데이터의 속성이 2개만 있다면 결정 경계는 선으로 표현된다.

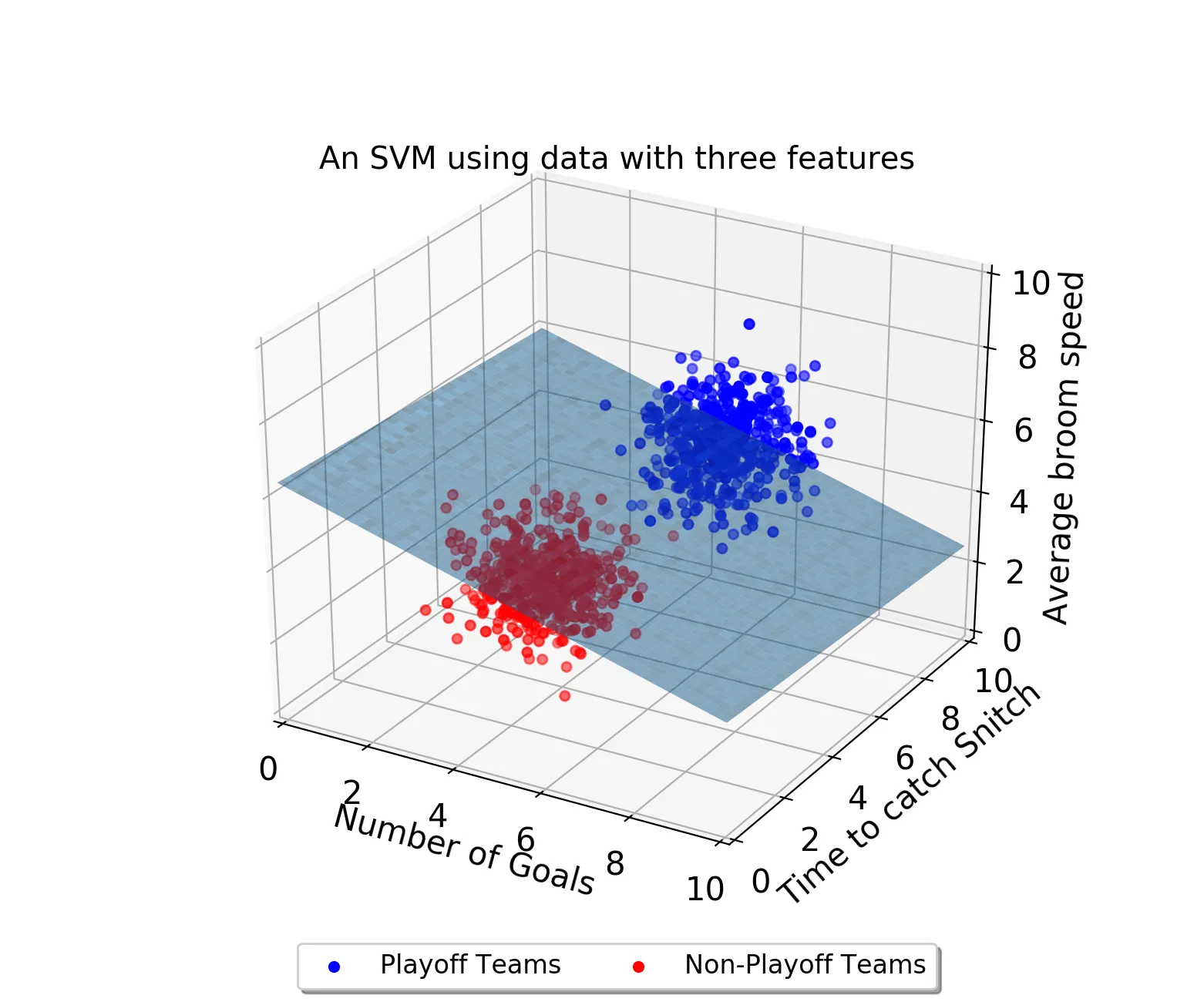
속성이 3개 라면 3차원으로 표시되고 다음과 같이 결정 경계는 평면이 된다.

속성이 4개 이상이되면 이제 고차원으로 넘어가기 때문에 결정 경계를 초평면이라고 부르게 된다.

최적의 결정 경계

결정 경계는 무수히 많기 때문에 어떤 것을 결정 경계로 사용해야 하는지 결정하는 것이 중요하다.

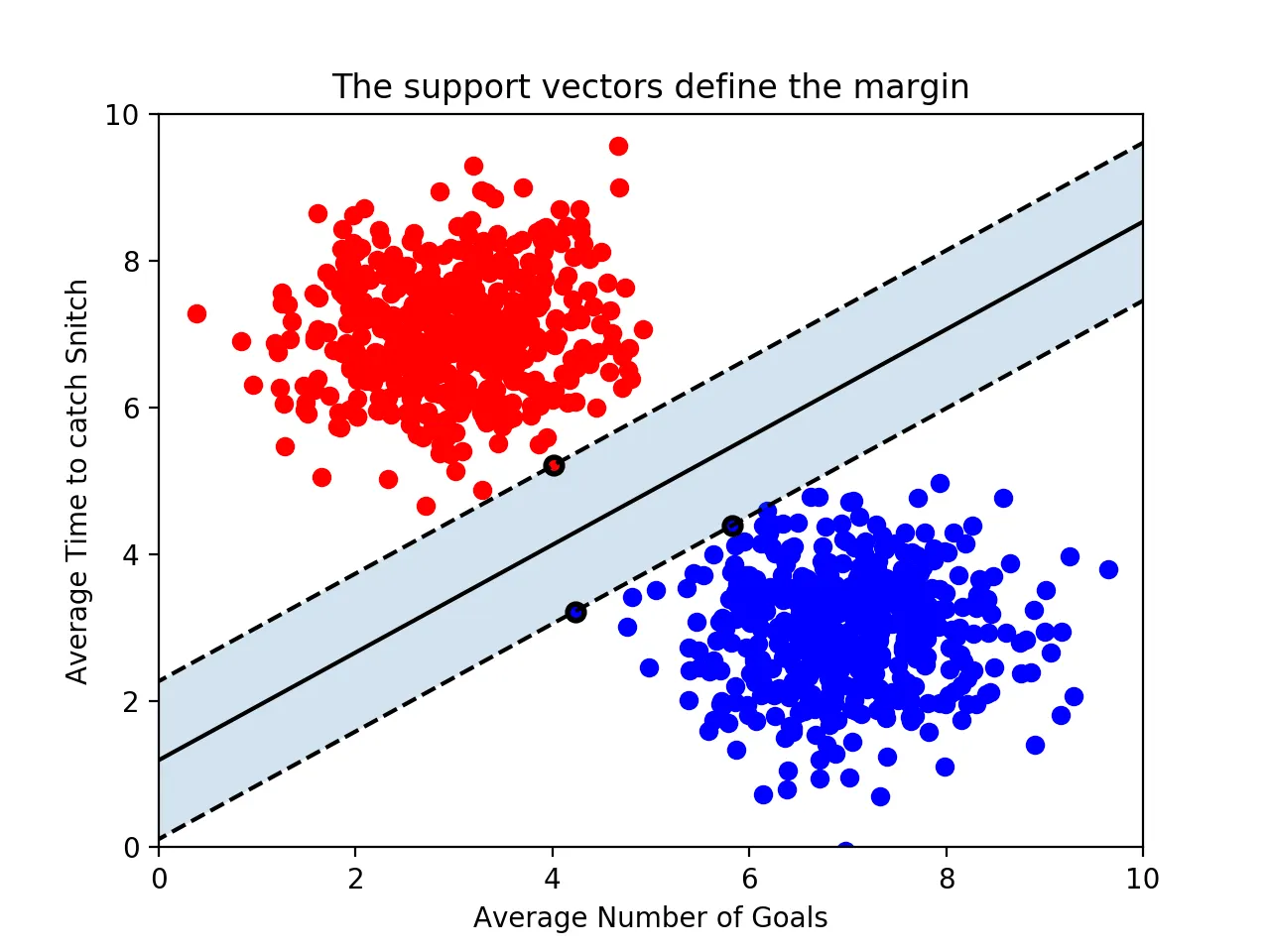
기본적으로 결정 경계는 데이터 군으로부터 최대한 멀리 떨어지는 것이 좋다. support vectors라는 의미는 결정 경계와 가장 가까이 있는 데이터 포인트를 말한다. 이 데이터들이 결정 경계를 정의하는 가장 결정적이 역할을 하게 된다.

마진

결정경계와 서포트 벡터 사이의 거리를 의미한다.

여기서 최적의 결정 경계는 앞서 말했듯이 데이터들로부터 멀리 떨어질수록 좋다고 했다.

따라서 마진을 최대화하는 결정 경계가 최적의 결정 경계가 된다.

위의 그림에서 볼 수 있듯이 속성이 2개인 데이터로부터 결정 경계를 결정하기 위해서는 최소 3개의 서포트 벡터가 필요한다.

즉, n개의 속성을 가진 데이터에는 최소 n+1개의 서포트 벡터가 존재해야 한다는 것을 알 수 있다.

여기서 SVM 의 장점이 드러나는데, 다른 분류 모델들은 모델을 학습하는데 학습 데이터를 모두 사용한다. 하지만 SVM은 결정 경계를 정의하는 데 필요한 데이터들이 서포트 벡터뿐이기 때문에 나머지 데이터들은 무시해도 된다. 따라서 매우 빠르게 처리 가능하다.

Scikit-learn 에서의 사용법

기본적인 svm 모델을 scikit-learn 패키지를 사용해서 구현해보자.

from sklearn.svm import SVC

classifier = SVC(kernel='linear')

training_points = [[1, 2], [1, 5], [2, 2], [7, 5], [9, 4], [8, 2]]
labels = [1, 1, 1, 0, 0, 0]

classifier.fit(training_points, labels) # 학습

classifier.predict([[3,2]]) # 예측

classifier.support_vectors_ #결정 경계를 정의하는 서포트 벡터
SQL
복사

이상치를 얼마나 허용할 것인가

타 분류 모델과 마찬가지로 이상치를 처리하는 것이 중요하다.

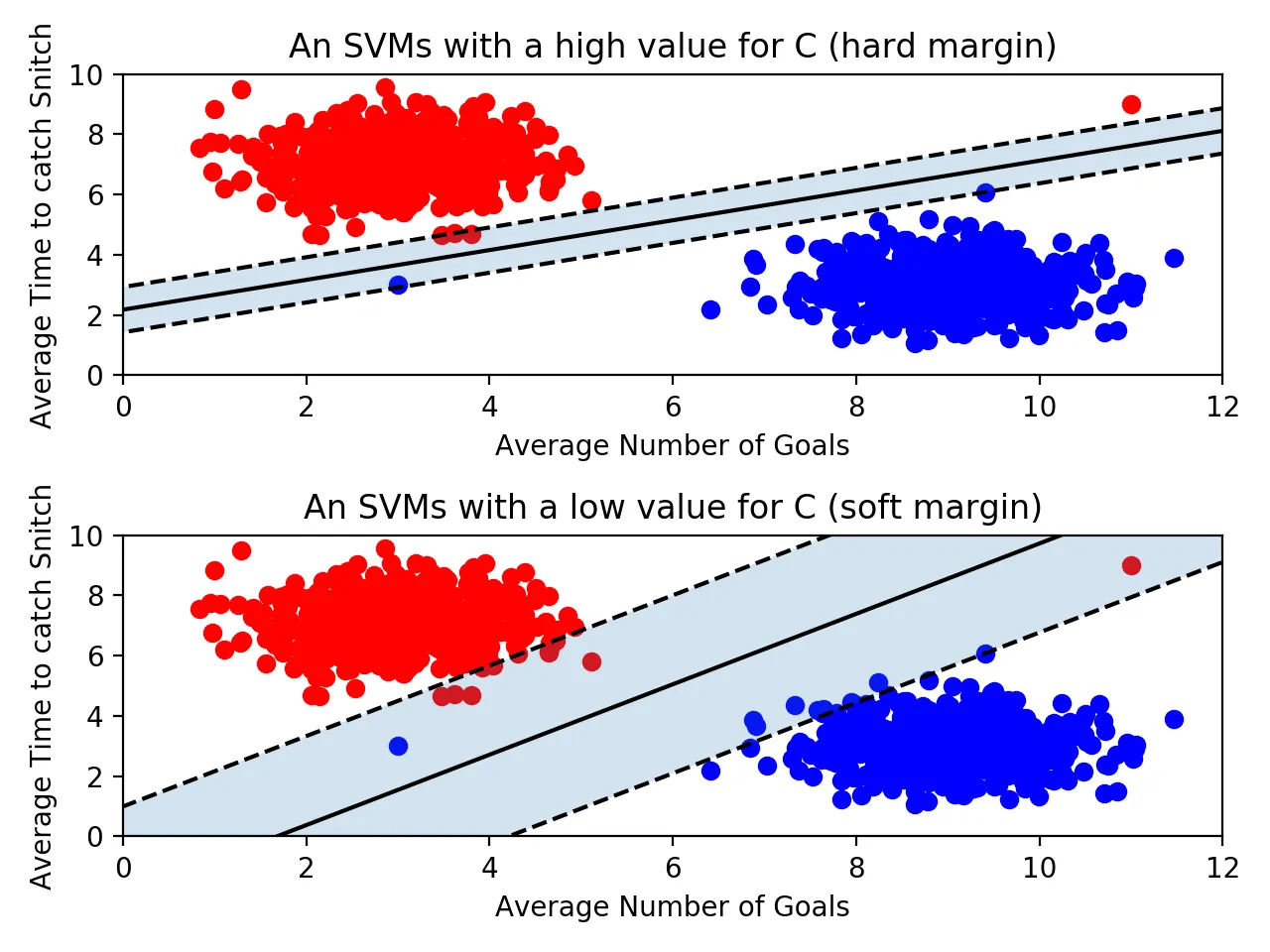
먼저, 아웃라이어를 허용하지 않는 기준으로 빡세게 결정 경계를 정의하는 것을 하드 마진이라고 부른다. 즉, 마진이 매우 좁아지고 개별적인 학습 데이터를 모두 고려하기 때문에 과적합의 문제가 발생할 수 있다.

반면, 아웃라이어를 마진 안에 허용함으로써 기준을 넉넉히 정의하는 것을 소프트 마진이라고 부른다. 즉 마진이 커지게 된다. 하지만 또 언더피팅의 문제가 발생할 수 있다.

파라미터 C

scikit-learn 모델에서 C는 위의 이상치를 얼마나 허용할 것인지 지정할 수 있는 파라미터다. C값이 클수록 이상치를 허용하지 않는것이고(하드마진), 작을수록 소프트 마진이다.

•

너무 크면 과대적합, 너무 작으면 정확도 떨어짐

•

기본값 1

C의 최적 값은 데이터에 따라 다르다. GridSearchCV를 통해서 찾아나가거나 해야 한다.

classifier = SVC(C=0.01) 
SQL
복사

커널

선형으로 결정 경계를 그을 수 없다면, scikit-learn의 kernel를 지정하여 해결하면 된다.

‘poly’ 같은 것을 넣어주면 된다.

classifier = SVC(kernel='poly')
SQL
복사

다만, 선형 말고 다른 커널을 사용할 때 주의해야 될 점이 있다. 단순히 이상치때문에 선형으로 분리할 수 없다고 판단해서 선형 아닌 커널을 사용하면 안된다. —> 과적합의 위험

커널 - 다항식

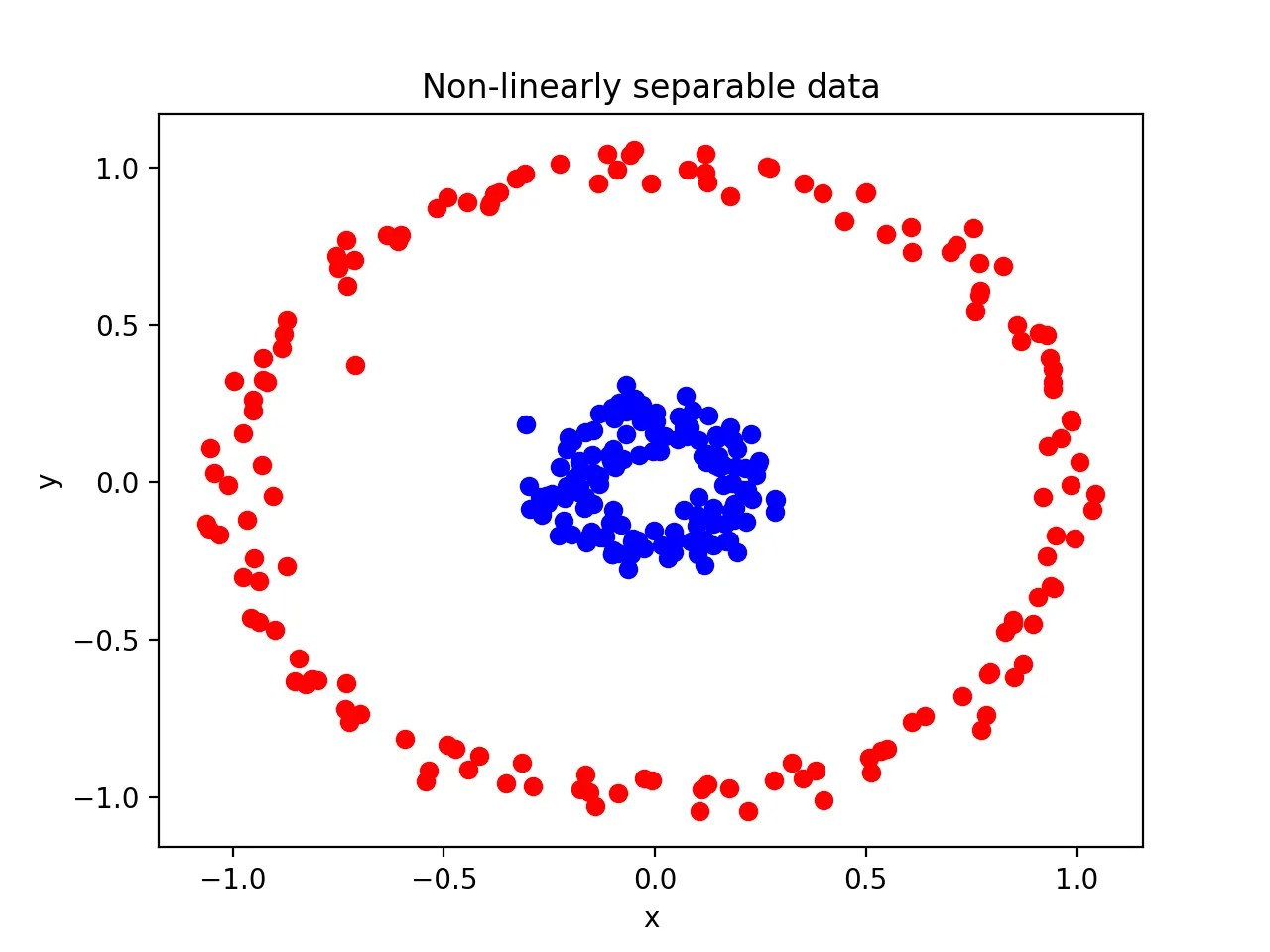
다음과 같은 극단적인 형태의 데이터가 있다고 하자. 당연히 선형으로 해결이 안되기 때문에

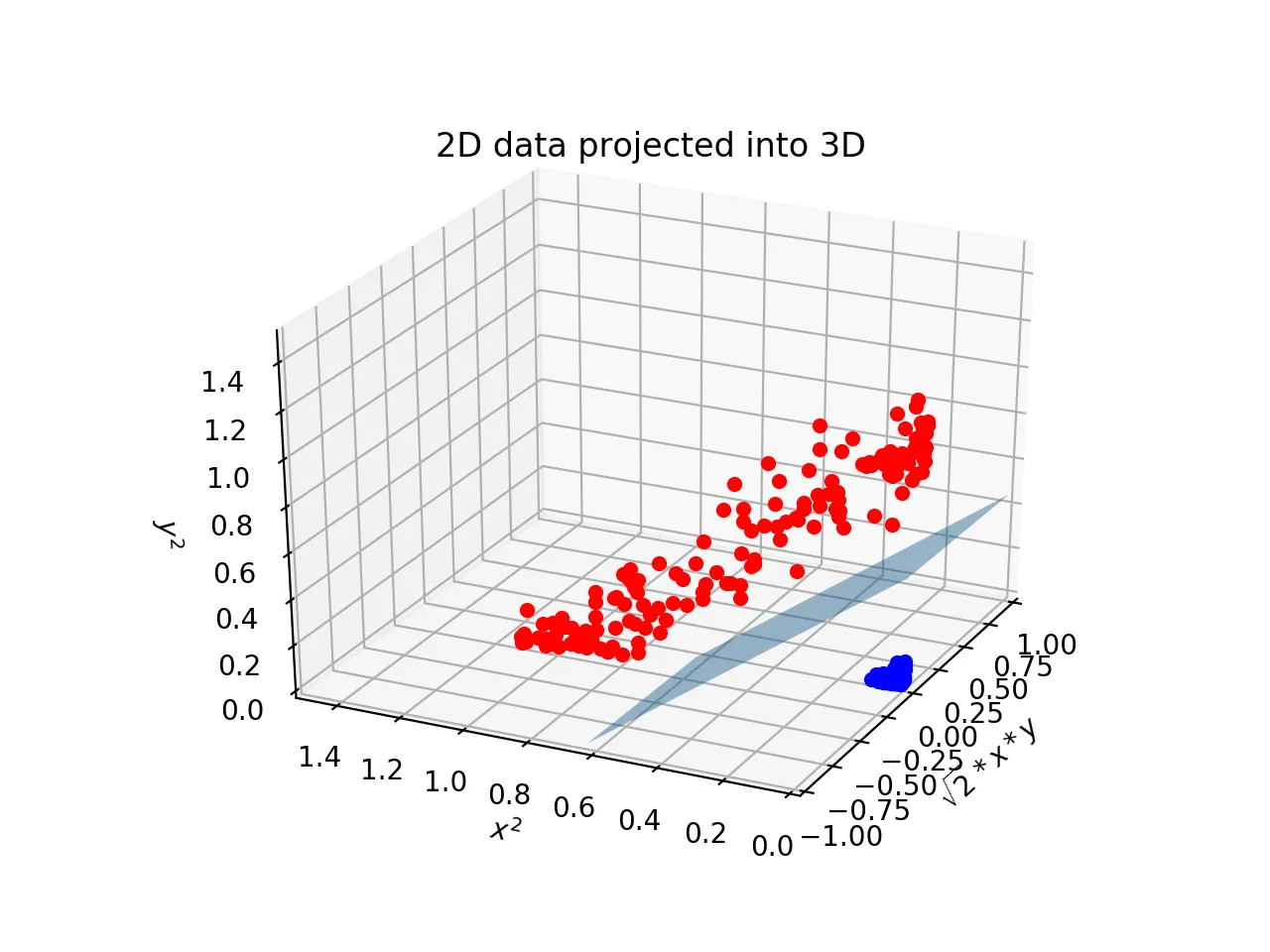
다항식 커널을 사용하면 된다. —> 2차원이 아닌 3차원으로 표현하게 된다.

이렇게 다항식의 커널을 사용하면 데이터를 더 높은 차원으로 변형시켜 나타냄으로써 초평면의 결정 경계를 얻어낼 수 있다.

커널 - 방사 기저 함수

RBF커널 혹은 가우시안 커널이라고 부른다. kernel = ‘rbf’ 인데, kernel의 기본값이다.

RBF커널은 2차원의 점을 무한한 차원의 점으로 변환한다.

classifier = SVC() # default kernel = 'rbf'
SQL
복사

파라미터 gamma (rbf , poly, sigmoid 커널에 사용)

결정경계를 얼마나 유연하게 그을 것인지 정해주는 파라미터다. 즉, 학습 데이터에 얼마나 민감하게 반응할 것인지를 조정해주는 것으로 C와 비슷하다.

•

너무 크면 과대적합이고 너무 작으면 정확도가 떨어진다.

◦

‘scale’(기본값) : 1 / (피처수*데이터셋 분산)

◦

‘auto’ : 1 / 피처수

classifier = SVC(C=2, gamma=0.5)
SQL
복사

gamma값을 높이면 학습 데이터에 많이 의존한다. 과적합의 문제가 있다.

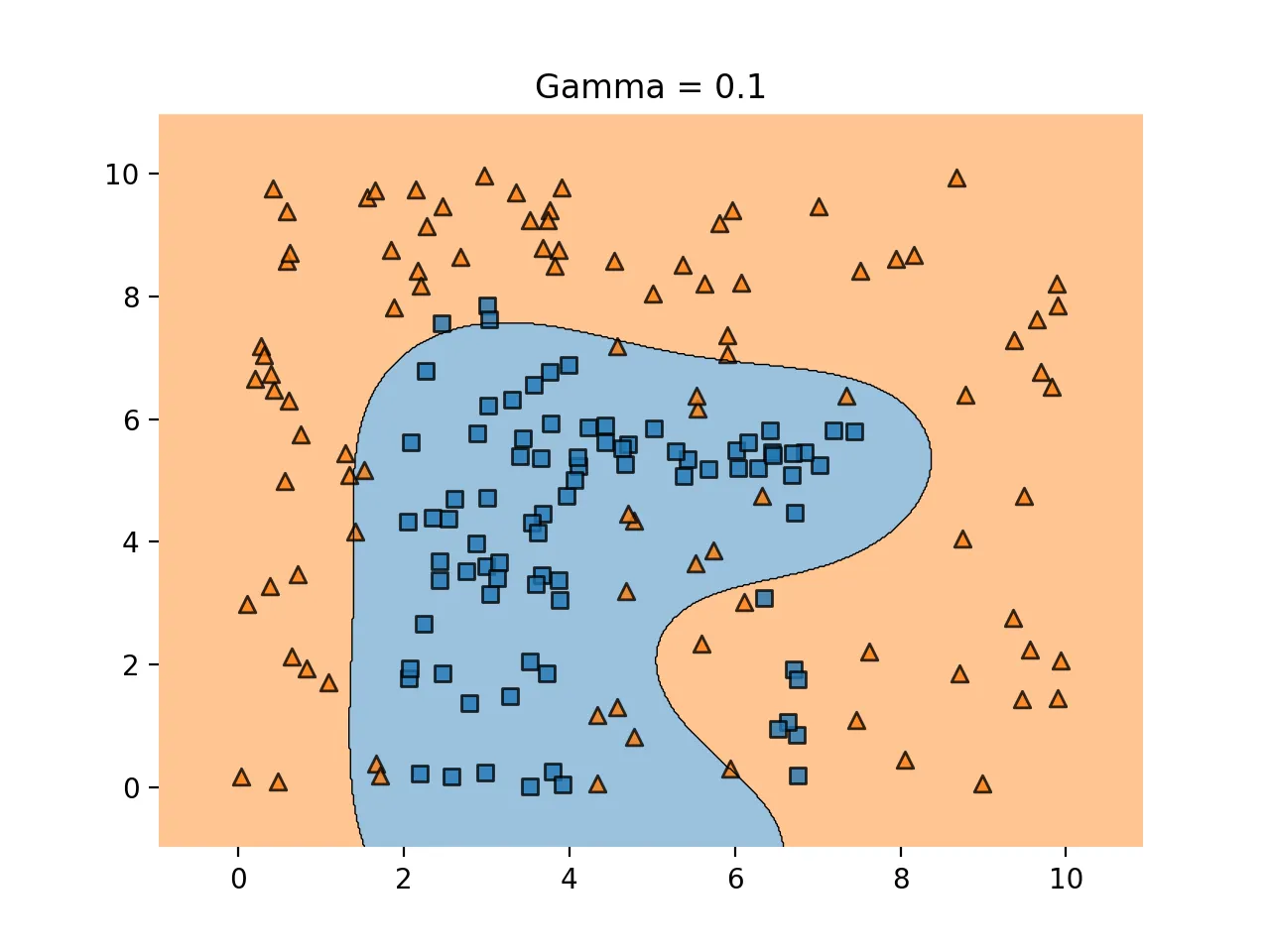
gamma값을 낮추면 학습 데이터에 많이 의존하지 않는다. 직선에 가깝게 결정경계를 생성한다. 언더피팅의 문제가 있다.

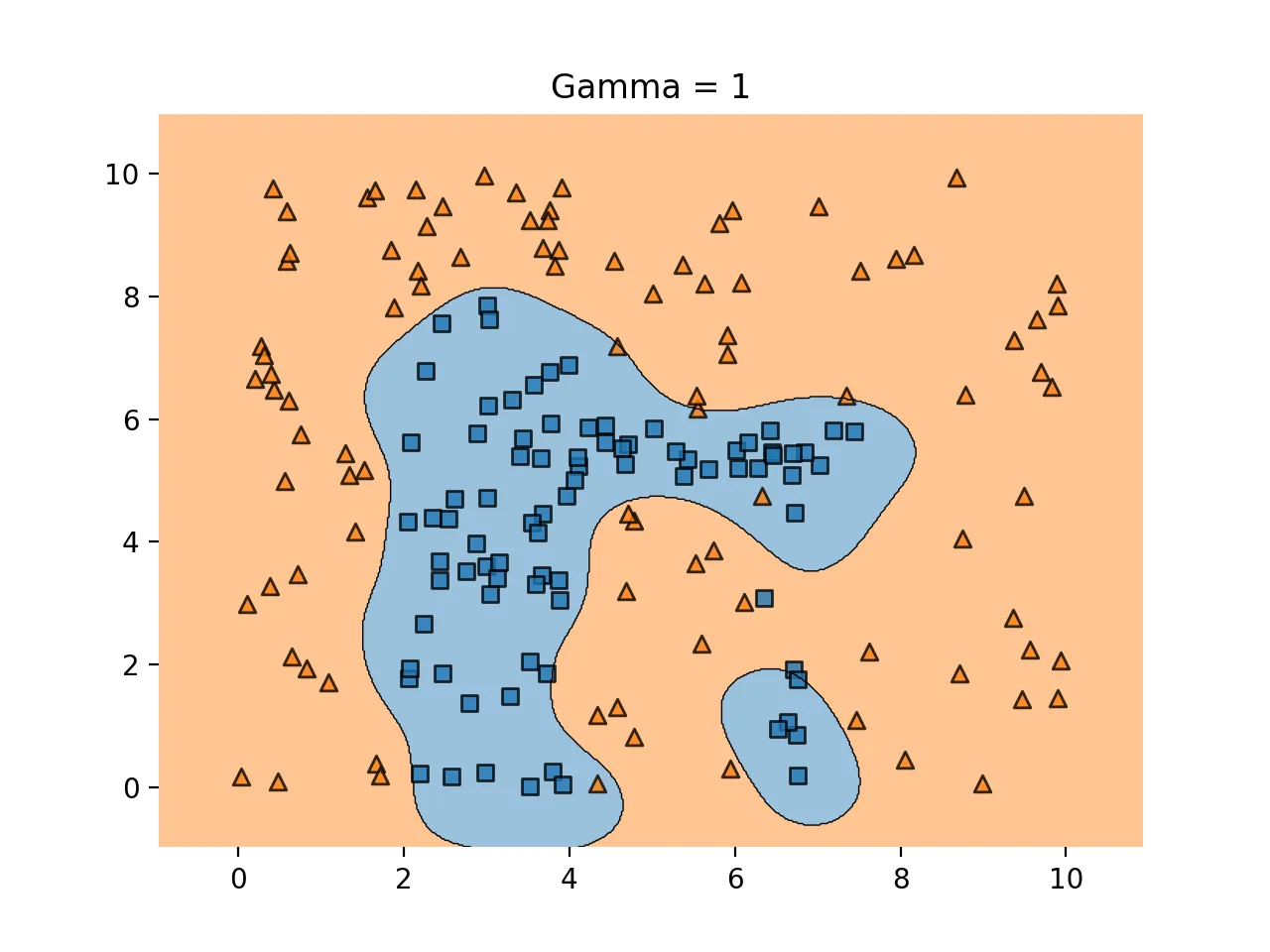
gamma 가 적당하면 다음과 같다.

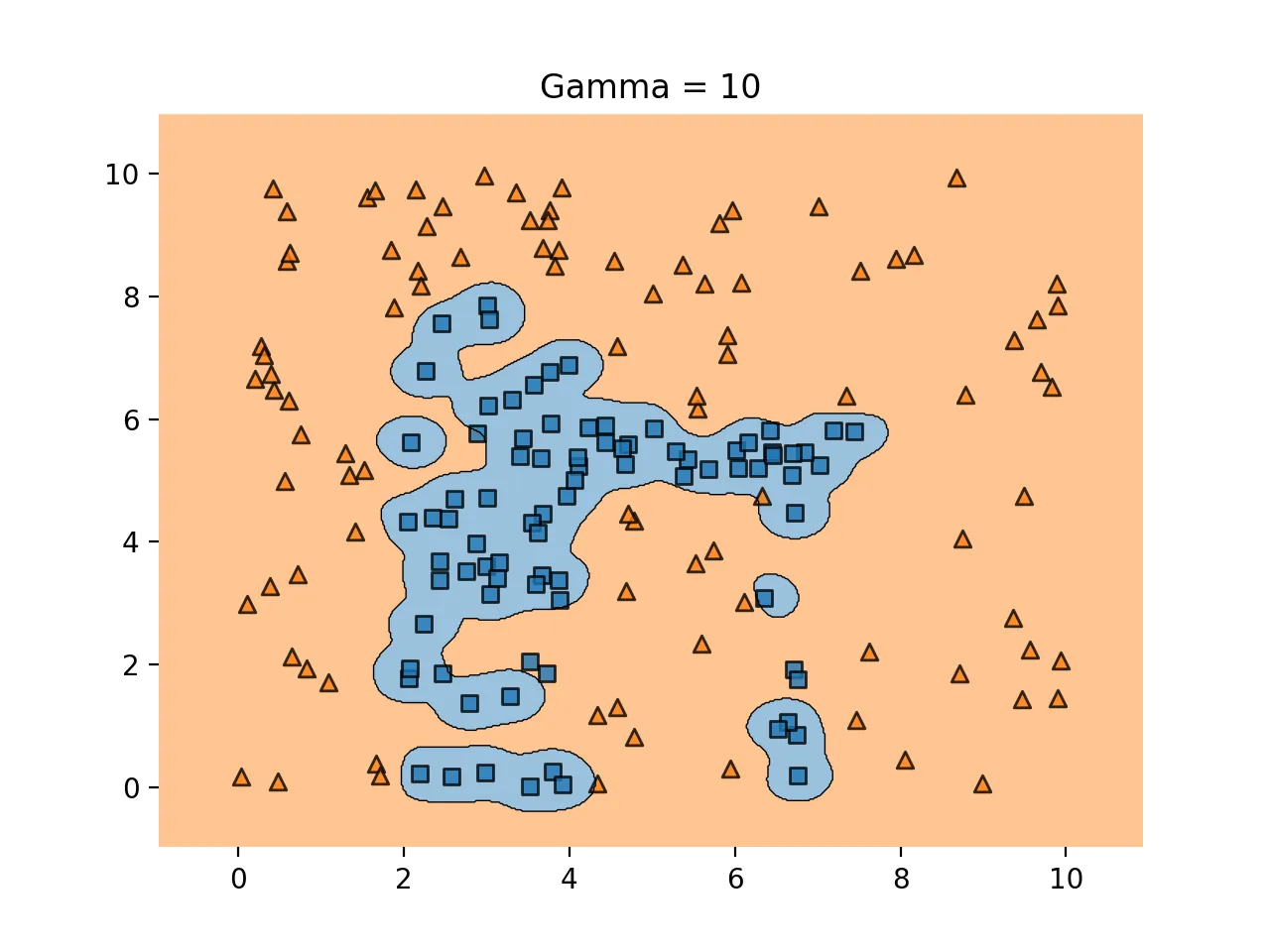
gamma를 너무 높이게 되면 다음과 같이 과적합 문제가 생긴다.

반대로 gamma를 너무 낮추게 되면 언더피팅의 문제가 생긴다.

scikit-learn 붓꽃 문제 적용

from sklearn.datasets import load_iris
iris = load_iris()
x1 = iris.data[:100,:2] # 100개의 데이터와, 2개의 변수만 활용
y1 = iris.target[:100] # 종속변수

from sklearn.svm import SVC
model1 = SVC(kernel='linear', C=1e10).fit(x1,y1) # C값이 10의 10승이므로 매우 큰 값. 하드마진 서포트벡터

# 예측 결과의 평가
from sklearn.metrics import classification_report
print(classification_report(y1,model1.predict(x1)))

# 결과
								precision    recall  f1-score   support

           0       1.00      1.00      1.00        50
           1       1.00      1.00      1.00        50

    accuracy                           1.00       100
   macro avg       1.00      1.00      1.00       100
weighted avg       1.00      1.00      1.00       100



	# 이번에는 C값을 0.1로 지정하여 다시 구해보자.
model2 = SVC(kernel='linear', C=0.1).fit(x1,y1)
print(classification_report(y1,model2.predict(x1)))

SQL
복사

서포트벡터머신의 장단점

장점

•

회귀와 분류 문제에 적용 모두 가능

•

예측력이 좋다. 

: 로지스틱 회귀나 판별 분석 같은 경우 데이터가 주어졌을 때 출력 라벨(yhat)에 대한 조건부 확률을 예측한다. 따라서 실제 라벨링을 할 때에는 조건부확률을 예측하고 임곗값도 정해야 한다. (2번의 추정이 필요) 하지만 서포트벡터머신은 확률이 아닌 라벨을 직접 추정하기 때문에 예측력이 높다고 한다.

단점

•

확률을 추정하지 못함

•

해석이 어렵다. 

커널이나 변환을 사용하는 경우 입력 변수와 출력 변수간 해석이 어려워진다.

stroke 데이터에 svm 활용

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid') 


# load data
df = pd.read_csv('D:me/jupyterNotebook/study/strokedata.csv')
df.drop('id', axis=1,inplace=True)
df.head()
df.info()
df.describe() 


###### data cleansing ######
# dealing with na
# 'bmi' 열의 null값을 mean으로 대체
df['bmi'] = df['bmi'].fillna(df['bmi'].mean())

# 'gender'내의 Other값을 가지고 있는 행 제거
other_index = df[df['gender']=='Other'].index
df = df.drop(other_index)


###### visualizing features ######
# 흡연여부, 직장, 거주지역이 stroke와의 연관성이 있을까?
# 확인해보기 위해 시각화를 진행한다.
import warnings
warnings.filterwarnings('ignore')
plt.figure(figsize=(21,5))

# 흡연여부 그래프 (stroke에 대한)
plt.subplot(1,3,1) # subplot 중 첫번째
sns.countplot(x=df['smoking_status'], alpha=0.8, palette='Paired', hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel('');
plt.title('Smoking Status');

# 직장 타입
plt.subplot(1,3,2)
sns.countplot(x=df['work_type'], alpha=0.8, palette='Paired', hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel=('');
plt.title('Work Type');

# 거주 지역
plt.subplot(1,3,3)
sns.countplot(x=df['Residence_type'], alpha=0.8, palette='Paired', hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel=('');
plt.title('Residence Type');
--> 그림으로써는 큰 영향이 있는 것으로 판단되지 않는다.


#성별, 고혈압의여부, 심장병의 여부 가 stroke와의 연관성이 있을까?
plt.figure(figsize=(21,5))

plt.subplot(1,3,1)
sns.countplot(x=df['gender'], alpha=0.8, palette='Paired',hue=df['stroke']);
# 틱과 경계선을 한꺼번에 설정
plt.tick_params(axis='both', which='both',bottom=False, left=True, right=False, top=False, labelbottom=True, labelleft=True); 
# Remove the top and right spines from plot(s)
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel=('')
plt.title('Gender, F/M : 59/41 %');

plt.subplot(1,3,2)
sns.countplot(x=df['hypertension'], alpha=0.8, palette='Paired',hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel=('')
plt.title('Hypertension');

plt.subplot(1,3,3)
sns.countplot(x=df['heart_disease'], alpha=0.8, palette='Paired',hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel=('');
plt.title('Heart Disease');


# 나이, 평균 Glucose level, bmi 가 stroke와의 연관성이 있을까?
sns.set_style('white')
plt.figure(figsize=(21,5))

plt.subplot(1,3,1)
sns.kdeplot(x=df['age'], alpha=0.2, palette='Set1', label='Smoker', fill=True, linewidth=1.5, hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=True, bottom=True, offset=None, trim=False);
plt.xlabel('');
plt.title('Age Distribution');

plt.subplot(1,3,2)
sns.kdeplot(x=df['avg_glucose_level'], alpha=0.2, palette='Set1', label='avg_glucose_level', linewidth=1.5, fill=True, hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=True, bottom=True, offset=None, trim=False);
plt.xlabel('');
plt.title('Average Glucose Level');

plt.subplot(1,3,3)
sns.kdeplot(x=df['bmi'], alpha=0.2, palette='Set1', label='BMI', shade=True, linewidth=1.5, hue=df['stroke']);
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=True, offset=None, trim=False);
plt.xlabel('')
plt.title('BMI');
SQL
복사

→ age가 확실히 영향력있는 변수인 것으로 확인된다.

# stroke 종속변수의 불균형적인 분포를 확인 --> 후에 오버샘플링이 필요
df['stroke'].value_counts()
SQL
복사

###### preprocessing data ######
# 범주형 데이터 --> 수치화
df['gender'] = df['gender'].replace({'Male':0, 'Female':1, 'Other':-1}).astype(np.uint8)
df['Residence_type'] = df['Residence_type'].replace({'Rural':0, 'Urban':1}).astype(np.uint8)
df['work_type'] = df['work_type'].replace({'Private':0, 'Self-employed':1, 'Govt_job':2, 'children':-1, 'Never_worked':-2}).astype(np.uint8)
df['ever_married'] = df['ever_married'].replace({'Yes':1, 'No':0}).astype(np.uint8)
df['smoking_status'] = df['smoking_status'].replace({'never smoked':0, 'Unknown':1, 'formerly smoked':2, 'smokes':-1}).astype(np.uint8)
SQL
복사

###### Model building ####### 
X = df.drop('stroke', axis=1)
y = df.pop('stroke')


# using SVM Classifier
# using pipeline
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, LabelEncoder # for onehot encoding, standardardiation
svm_pipeline = Pipeline(steps=[('scale',StandardScaler()), ('SVM',SVC(random_state=0. probability = True))])
SQL
복사

# 학습 데이터 / 테스트 데이터 나누기
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y) # default
y_train.shape

# 불균형 레이블 처리하기
# using SMOTE for oversampling
from imblearn.over_sampling import SMOTE
oversample = SMOTE()
X_train_resh, y_train_resh = oversample.fit_resample(X_train,y_train.ravel())
SQL
복사

교차 검증을 수행한다. cv=10 으로 우선 적용한다. 평가 지표는 f1 score로 진행한다.

from sklearn.model_selection import cross_val_score
svm_cv = cross_val_score(svm_pipeline, X_train_resh, y_train_resh, cv=10, scoring='f1')
svm_cv.mean()


###### model evaluation ######
from sklearn.metrics import confusion_matrix
svm_pipeline.fit(X_train_resh, y_train_resh); # 오버샘플링한 데이터로 학습
svm_train_predict = svm_pipeline.predict(X_train) # 예측은 오버샘플링 전 x 데이터
svm_pred = svm_pipeline.predict(X_test) # 테스트 데이터 예측
svm_cm = confusion_matrix(y_train,svm_train_predict) # train데이터에 대한 오차행렬

from sklearn.metrics import roc_curve, auc
fpr_lr, tpr_lr = roc_curve(y_test, svm_pipeline.predict_proba(X_test)[:,1]) # test데이터에 대한 roc_curve

plt.figure(figsize=(12,8));

plt.plot(fpr_lr, tpr_lr);
plt.xlabel('False Positive Rate', fontsize=16);
plt.ylabel('True Positive Rate', fontsize=16);
plt.title('ROC curve', fontsize=16);
plt.plot([0,1],[0,1], color='navy', lw=3, linestyle='--');
sns.despine(fig=None, ax=None, top=True, right=True, left=False, bottom=False, offset=None, trim=False);

print('Auc : ', auc(fpr_lr, tpr_lr))

from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score
print(classification_report(y_test,svm_pred))

print('Accuracy Score : ', accuracy_score(y_test,svm_pred))
print('F1 Score : ', f1_score(y_test,svm_pred))
SQL
복사

###### Grid Search Tunning ######
from sklearn.model_selection import GridSearchCV
param_grid = {'C':[0.1,1,10,1000], 'gamma':[1,0.1,0.01,0.001]}
grid = GridSearchCV(SVC(), param_grid, verbose=3)

# fit the data
grid.fit(X_train_resh,y_train_resh)

# best parameters based on param grid
grid.best_params_

# grid_model with best parameters
grid.best_estimator_

grid_train_predict = grid.predict(X_train)
grid_pred = grid.predict(X_test)

# evaluation of grid
classification_report(y_test,grid_pred)
classification_report(y_train,grid_train_predict)
SQL
복사