→ 그래프 탐색 알고리즘.
‘탐색’이란 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정을 말한다.
그 중 대표적인 탐색 알고리즘이 DFS / BFS 다.
재귀함수 → dfs 알고리즘에서 주로 사용
재귀함수는 dfs, bfs 알고리즘을 구현할 때 많이 사용하는 구조이기 때문에 알고 있어야 한다.
재귀함수는 특히 코딩테스트 같은 경우, 종료 조건을 반드시 명시해줘야 한다.
def recursive_function(i):
# 100번째 호출을 했을 때 종료되도록 종료 조건 명시
if i==100:
return
print(i, "번째 재귀함수에서", i+1, '번째 재귀함수를 호출합니다.')
recursive_function(i+1)
print(i, '번째 재귀함수를 종료합니다.')
recursive_function(1)
Python
복사
•
팩토리얼 구현 예제
# 반복적으로 구현한 n!
def factorial_iterative(n):
result = 1
# 1부터 n까지의 수를 차례대로 곱하기
for i in range(1,n+1):
result *= i
return result
# 재귀적으로 구현한 n!
def factorial_recursive(n):
if n <= 1: # n이 1이하인 경우 1을 반환
return 1
# n! = n * (n-1)! 를 그대로 코드에 구현
return n * factorial_recursive(n-1)
# 각각의 방식으로 구현한 n! 출력(n=5)
print('반복적으로 구현:', factorial_iterative(5))
print('재귀적으로 구현:', factorial_recursive(5))
Python
복사
•
최대공약수 계산 예제
두 개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘으로는 유클리드 호제법이 있다.
◦
유클리드 호제법
→ 두 자연수 A,B 에 대하여 (A>B) A를 B로 나눈 나머지를 R 라고 하자
→ 이때 A와 B의 최대공약수는 B와 R의 최대공약수와 같다.
# 유클리드 호제법
# 1. 위의 과정을 반복하면서 최대공약수의 결과는 B가 A의 약수일 때 B가 된다.
def gcd(a,b):
if a % b == 0:
return b
else:
return gcd(b, a % b)
print(gcd(192,162))
Python
복사
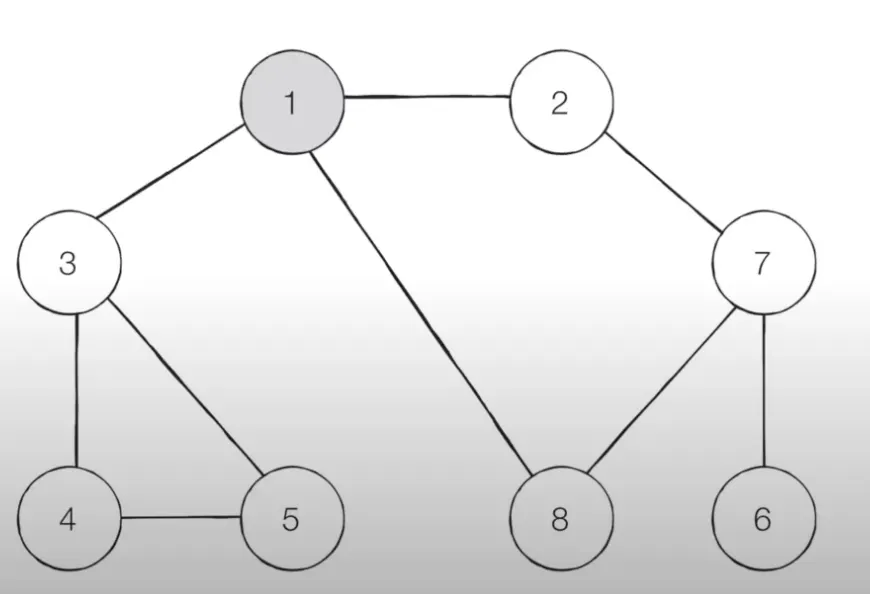
DFS(depth-first search)
깊이 우선 탐색. 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.
스택 자료구조(혹은 재귀 함수)를 이용하며, 구체적인 동작 과정은 아래와 같다.
1.
탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2.
스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접한 노드가 없으면 최상단 노드를 꺼낸다.
3.
더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
→ 인접한 노드가 여러 개일때 방문 기준?
문제의 상황마다 다르고 때에 따라서는 상관 없을 수도 있다. 일반적으로는 번호가 낮은 인접 노드부터 방문한다.
[step1] 시작 노드인 ‘1’을 스택에 삽입하고 방문 처리한다.
[step2] 스택의 최상단 노드인 ‘1’에 방문하지 않은 인접노드 ‘2’, ‘3’, ‘8’ 이 있다. 이 중에서 가장 작은 노드인 ‘2’를 스택에 넣고 방문 처리 한다.
[step3] 스택의 최상단 노드인 ‘2’에 방문하지 않은 인접노드는 ‘7’이 있다. 따라서, ‘7’번 노드를 스택에 넣고 방문 처리 한다.
[step4] 스택의 최상단 노드인 ‘7’에 방문하지 않은 인접노드는 ‘6’ ,’8’ 이 있다. 이 중에서 가장 작은 노드인 ‘6’을 스택에 넣고 방문 처리 한다.
[step5] 스택의 최상단 노드인 ‘6’에 방문하지 않은 인접노드가 없다. 따라서 스택에서 ‘6’을 꺼낸다.
[step6] 스택의 최상단 노드인 ‘7’에 방문하지 않은 인접노드 ‘8’이 있다. 따라서 ‘8’번 노드를 스택에 넣고 방문 처리 한다.
→ 이런 과정을 반복했을 때 전체 노드의 탐색 순서(스택에 들어간 순서)는 아래와 같다.
탐색 순서 : 1 → 2 → 7 → 6 → 8 → 3 → 4 → 5
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
visited = [False]*9
def dfs(graph,v,visited):
# 현재 노드를 방문 처리
visited[v] = True
print(v, end=' ')
# 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for i in graph[v]:
if not visited[i]:
dfs(graph,i,visited)
Python
복사
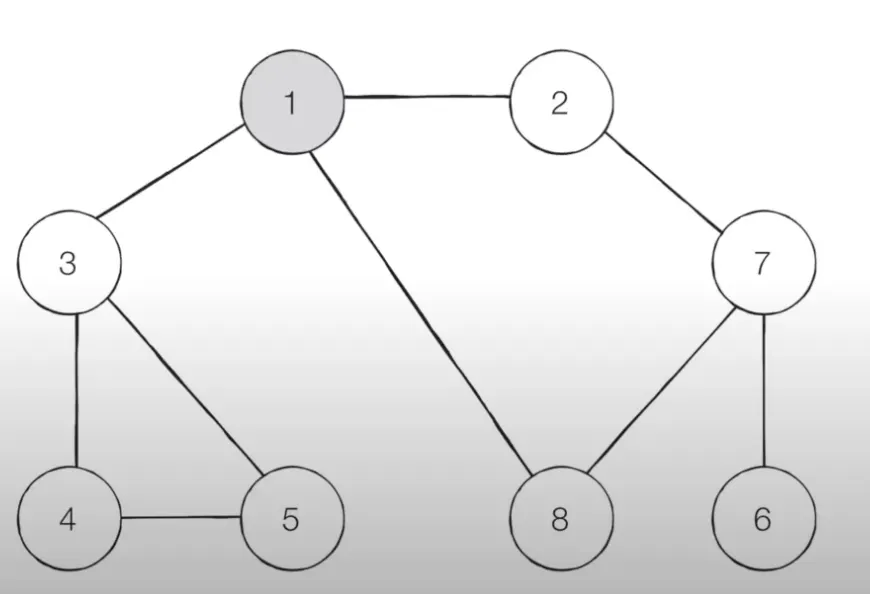
BFS(breadth first search)
‘너비 우선 탐색’ 이라는 의미를 가진다. 가까운 노드부터 탐색하는 알고리즘이다.( DFS)
DFS)
BFS 구현에서는 선입선출 방식인 큐 자료구조를 이용하는 것이 정석이다. 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어 가까운 노드부터 탐색을 진행하게 된다.
1.
탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2.
큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리 한다.
3.
2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
[step1] 시작 노드인 ‘1’을 큐에 삽입하고 방문 처리 한다.
[step2] 큐에서 노드 ‘1’을 꺼내고 방문하지 않은 인접 노드 ‘2’, ‘3’, ‘8’ 을 모두 큐에 삽입하고 방문 처리 한다.
[step3] 큐에서 노드 ‘2’를 꺼내고 방문하지 않은 인접 노드 ‘7’을 큐에 삽입하고 방문 처리 한다.
[step4] 큐에서 노드 ‘3’을 꺼내고 방문하지 않은 인접 노드 ‘4’ 와 ‘5’를 모두 큐에 삽입하고 방문 처리 한다.
[step5] 큐에서 노드 ‘8’을 꺼내고 방문하지 않은 인접 노드가 없으므로 무시한다.
[step6] 큐에서 노드 ‘7’을 꺼내고 방문하지 않은 인접 노드 ‘6’을 큐에 삽입하고 방문 처리 한다.
[step7] 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 차례대로 꺼내면 최종적으로 다음과 같다.
1 → 2 → 3 → 8 → 7 → 4 → 5 → 6
구현함에 있어 앞서 언급한 deque 라이브러리를 사용하는 것이 좋고, 탐색 수행 시간은 O(N) 시간이 소요된다. 실제 수행 시간은 DFS 보다 좋은 편이다. 즉, 코딩 테스트에서는 보통 DFS 보다 BFS 구현이 조금 더 빠르게 동작한다는 것만 기억하자.
from collections import deque
# 각 노드가 연결된 정보를 리스트 자료형으로 표현(2차원 리스트)
graph = [
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
# 각 노드가 방문된 정보를 리스트 자료형으로 표현(1차원 리스트)
visited = [False]*9
# BFS 메서드 정의
def bfs(graph, start, visited):
# 큐 구현을 위해 deque 라이브러리 사용
queue = deque([start]) # 들어온 노드를 큐에 저장
# 현재 노드를 방문 처리
visited[start] = True
# 큐가 빌 때까지 반복
while queue:
# 큐에서 하나의 원소를 뽑아 출력
v = queue.popleft()
print(v, end = ' ')
# 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for i in graph[v]
Python
복사
BFS 문제
import sys
from collections import deque
M, N = map(int, sys.stdin.readline().split())
graph = [list(map(int, input().split())) for _ in range(M)] # 첫행부터 끝행까지 N개의 데이터를 리스트로 입력받는다.
visited = [[-1] * N for _ in range(M)] # 방문 처리 표시할 MxN 2차원 리스트 생성
# 상 우상 우 우하 하 좌하 좌 좌상 : 배열에서의 방향에 따른 인덱스 변화 값들
dx = [-1, -1, 0, 1, 1, 1, 0, -1]
dy = [0, 1, 1, 1, 0, -1, -1, -1]
queue = deque()
def bfs(i,j):
queue.append((i,j)) # 큐에 들어온 값의 위치 저장
visited[i][j] = 0 # 방문처리 -> 방문처리를 0으로 해야 나중에 중복해서 탐색하지 않는다.
while queue: # 큐에 값이 없을때까지 반복
x, y = queue.popleft() # 큐에서 현재 위치 값 삭제하면서 값 추출
for i in range(8): # 8방향(인접한 노드의 수)에 대해서 bfs 탐색
nx = dx[i] + x # 이동한 x 위치
ny = dy[i] + y # 이동한 y 위치
if 0 <= nx < M and 0 <= ny < N and visited[nx][ny] == -1 and graph[nx][ny] == 1:
visited[nx][ny] = 0 # 방문처리
queue.append((nx,ny))
word = 0
for i in range(M):
for j in range(N): # 행렬에서 차례대로 탐색해나간다
if graph[i][j] == 1 and visited[i][j] == -1: # 값이 1이면서 방문하지 않았다면
bfs(i,j) # bfs 수행
word += 1
print(word)
Python
복사
•
“if 0 <= nx < M and 0 <= ny < N and visited[nx][ny] == -1 and graph[nx][ny] == 1” 의 조건 해석
◦
현재 움직인 위치 nx, ny가 제한된 범위를 벗어나지 않았는지 확인
→ 0 <= nx < M and 0 <= ny < N
◦
아직 방문하지 않았고 값이 1인지 확인
→ visited[nx][ny] == -1 and graph[nx][ny] == 1