결측치에 대한 개념, 종류, 처리 방법에 대한 내용을 다룬다.
결측치 개념
•
결측치 : NaN, Null, NA
•
판다스 : None, NaN
•
넘파이 : np.nan
결측치 종류
결측치에는 크게 완전 무작위 결측(MCAR) 와 무작위 결측(MAR) , 비무작위 결측(MNAR) 이 있다.
1.
완전 무작위 결측(Missing Completely at Random ; MCAR)
: 어떤 변수의 결측치가 무작위로 발생한 경우 (다른 변수와 관련 X )
2.
무작위 결측(Missing at Random ; MAR)
: 어떤 변수의 결측치 여부가 다른 변수와 관련이 있는 경우 (값의 상관관계는 알 수 X)
3.
비무작위 결측(Missing Not at Random ; MNAR)
: 어떤 변수의 결측치값이 다른 변수와 관련이 있는 경우 (값의 상관관계 O)
결측치 처리 방법 개요
다양한 방법이 존재한다.
결측치 비율에 따른 결측치 처리 방법 선택
결측치 비율 | 결측치 처리 방법 |
10% 미만 | 제거 또는 대체 |
10% ~ 20% 미만 | 모델 기반 처리 |
20% 이상 | 모델 기반 처리 |
1. 제거
결측치가 있는 행이나 열을 제거하는 방법이다. 데이터 손실이 크다는 단점이 있기때문에 이런 경우는 거의 없다.
2. Heuristic Imputation
분석가가 보편적인 상식 또는 도메인 지식을 토대로 임의로 결측치를 대체하는 방법이다.
3. Mean/Median/Mode Imputation
결측치를 평균, 중앙값, 최빈값으로 대체하는 방법이다.
4. Prediction Model
모델을 통해 예측한 값으로 결측치를 대체하는 방법이다.
NA Imputation - deletion(수치형 변수 O/ 범주형 변수 O)
Deletion은 결측치를 제거하는 방법이다. 결측치가 적을 때 주로 사용한다. MCAR 를 가정한다. 쉽고, 원래의 분포를 보존한다는 장점이 있다. 하지만 데이터 손실이 생긴다는 점에서 데이터가 적을 경우에는 좋은 방법이 아니다. df.dropna(axis=0) 을 통해서 결측치가 있는 행을 제거한다. df.dropna(axis=1) 을 통해서 결측치가 있는 열을 제거한다.
NA Imputation - Mean/Median (수치형 변수 O/범주형 변수 X)
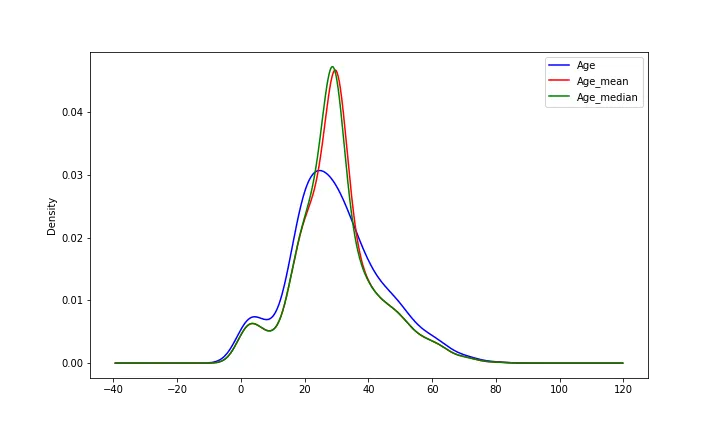
결측치를 해당 변수의 평균/중앙값으로 대체하는 방법이다. 일반적으로 과적합을 피하기 위해 train셋에서 결측치를 대체할 값을 구한 다음 이를 train셋과 test셋 모두 적용한다. MCAR을 마찬가지로 가정한다. 쉽고 빠르다는 장점이 있다. 하지만, 기존 분포의 분산을 변형시킬 가능성이 있다. (즉, 다른 변수와의 관계가 변형될 수 있다) df.fillna() 함수를 이용한다.
# 기존 분포의 분산과 결측치 대체한 분포의 분산 비교
print('Original Variance : ',df['Age'].std())
print('Variance after mean imputation : ',df['Age_mean'].std())
print('Variance after median imputation : ',df['Age_median'].std())
Original Variance: 14.526497332334042
Variance after mean imputation: 13.002301745416018
Variance after median imputation: 13.005010341761803
# 간단하게 분포의 분산 시각화 (곂쳐서 -> 비교되게)
fig, ax = plt.subplots(figsize=(10,6))
df['Age'].plot(kind='kde', ax=ax, color='blue')
df['Age_mean'].plot(kind='kde', ax=ax, color='red')
df['Age_median'].plot(kind='kde', ax=ax, color='green')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
NA Imputation - Random sample imputation(수치형 변수 O/범주형 변수 X)
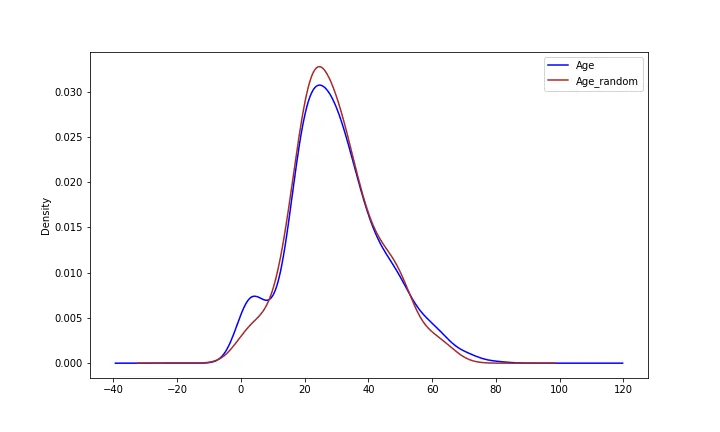
말 그대로 결측치를 해당 변수의 랜덤한 값으로 대체하는 방법이다. 대체한다는 것은 동일하나 원래의 분포를 유지할 수 있다는 점에서 다르다. 마찬가지로 MCAR 을 가정한다. 단점은 아무값으로 대체하기 때문에 좀 위험하다는 것이다. df.sample(n=결측치개수) 로 결측치를 랜덤한 값으로 대체한다.
# random sampling
df['Age_random'] = df['Age']
temp = (df['Age'].dropna().sample(df['Age'].isnull().sum())) # 결측치 개수만큼 랜덤 샘플링
temp.index = df[lambda x : x['Age'].isnull()].index # 결측치 인덱스를 부여
# NA Imputation
df.loc[df['Age'].isnull(),'Age_random'] = temp
# 확인
df[['Age','Age_random']].isnull().sum()
Age 177
Age_random 0
dtype: int64
# random한 값으로 대체한 후 분포를 기존분포와 시각적으로 비교
fig, ax = plt.subplots(figsize=(10,6))
df['Age'].plot(kind='kde', ax=ax, color='blue')
df['Age_random'].plot(kind='kde', ax=ax, color='red')
lines, labels = ax.get_legend_handles_labels()
ax.legend(lines, labels, loc='best')
Python
복사
NA Imputation - freqent category imputation(수치형 변수 X/ 범주형 변수 O)
결측치를 해당 변수에서 가장 빈도 수가 높은 범주로 대체하는 방법이다. MCAR을 가정한다. 원래의 분포를 변형시킬 수 있고, 결측치가 많을 경우 빈도 수가 높은 범주가 over-representation 될 수 있다는 단점이 있다.
# 범주별 빈도 수 확인
df['Embarked'].value_counts()
# na imputation
df['Embarked_filled'] = df['Embarked'].fillna(df['Embarked'].value_counts(ascending=False).index[0])
Python
복사
NA Imputation - adding a variable to capture NA(수치형 변수 O/범주형 변수 O)
결측치일때는 1을, 아닐때는 0을 갖는 변수를 새로 만든다. MCAR이 아님을 가정한다. 차원이 증가한다는 단점을 갖는다. np.where(df.isnull, 1, 0) 을 통해서 새로운 변수를 만들어 낸다.
수치형 변수에 대해서 imputation 을 진행해본다.
df['Age_isnull'] = np.where(df['Age'].isnull(),1,0) # 새로운 변수 정의
# 확인
df[['Age','Age_isnull']].isnull().sum()
Age 177
Age_isnull 0
dtype: int64
Python
복사
범주형 변수에 대해서 imputation을 진행해본다.
df['Embarked_isnull'] = np.where(df['Embarked'].isnull(),1,0)
# 확인
df[['Embarked','Embarked_isnull']].isnull().sum()
Embarked 2
Embarked_isnull 0
dtype: int64
Python
복사
NA Imputation - adding a category to capture NA(수치형 변수 X/ 범주형 변수 O)
결측치일 때 속하는 범주를 새롭게 생성할 수 있다. 주로 결측치가 많을 때 사용한다. 반면 결측치가 적을 경우 트리 기반 모델에서 과적합이 일어날 수 있다는 단점이 있다.