개요
이상치 탐지는 오류 식별과 함께 중요할 수 있는 데이터 포인트 발견 사이의 경계에 있음.
통계 기법과 알고리즘 접근법을 통해, z-score, IQR과 같은 단변량 방법부터 dbscan 과 lof과 같은 다변량 기법까지 다양한 이상치 탐지 방법의 이론과 응용을 학습
이상치의 유형
•
단변량 이상치
단 하나의 특성만 보고 이상치를 판단하는 경우
•
다변량 이상치
여러 특성값이 있는 상태에서 이상치를 판단하는 경우
단변량 이상치 탐지
•
z-score
데이터에서 표준 편차를 이용해 이상치를 감지하는 방법. 데이터를 표준화한 뒤, 각 데이터 포인트가 평균으로부터 얼만큼 떨어져있는가를 계산해 이상치를 식별.
•
IQR(사분위수범위)
데이터의 ‘중앙값’을 기준으로 ‘정상 범위’를 벗어난 데이터 포인트를 시각적으로 찾아냄. Q1(제1사분위수)와 Q3(제3사분위수)를 구한 뒤, 이를 기반으로 IQR을 계산해 이상치를 탐지
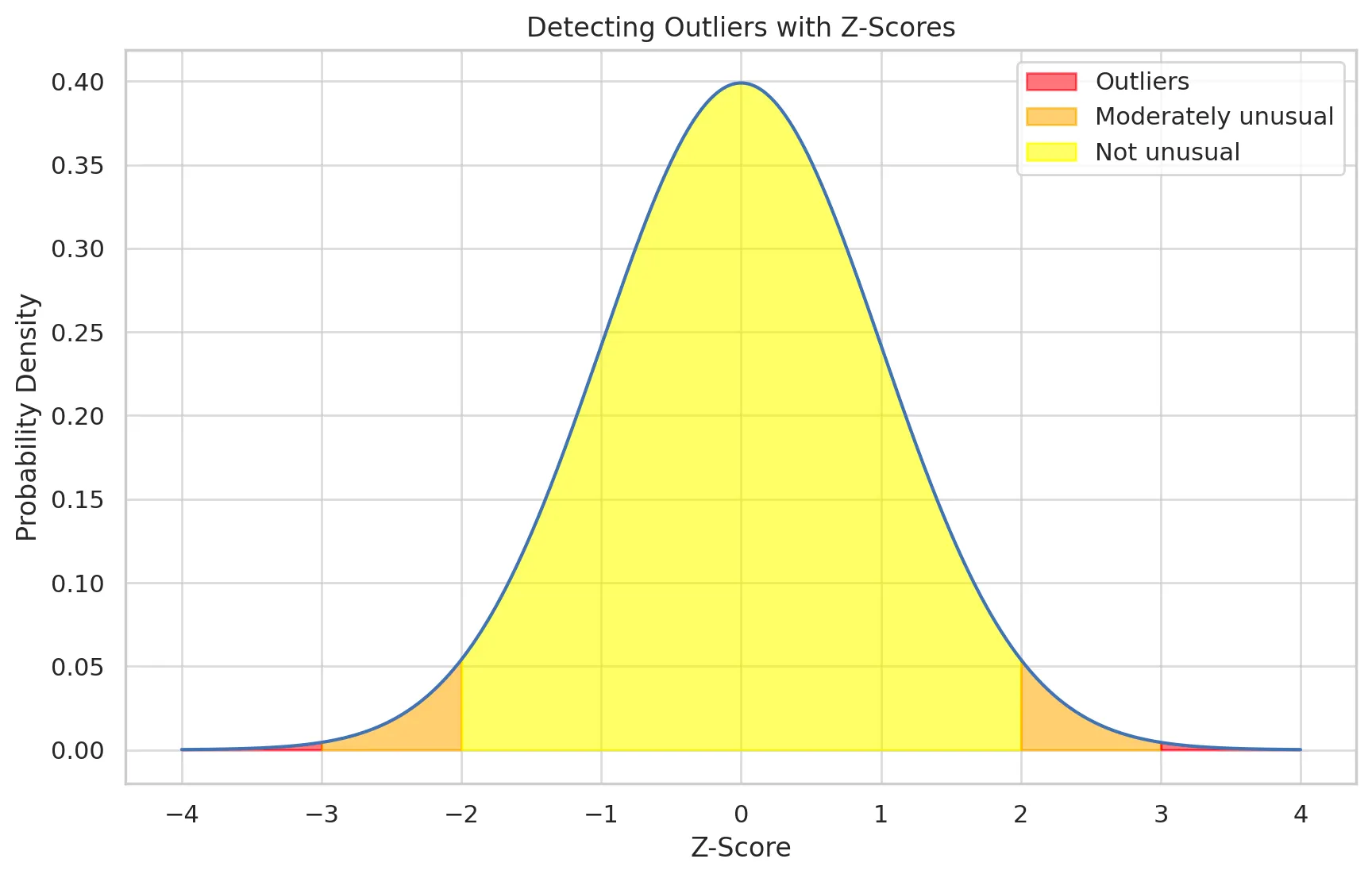
3.1. Z-Score의 해석
데이터가 정규 분포를 따른다고 가정할 경우 아래와 같이 해석할 수 있습니다.
•
Z-Score = 0: 데이터 포인트가 평균값에 정확히 일치
•
Z-Score > 0: 데이터 포인트가 평균값보다 높음
•
Z-Score < 0: 데이터 포인트가 평균값보다 낮음
→ 일반적으로, Z-Score가 매우 높거나 낮은 값(예를 들어, ±2 또는 ±3 이상)은 데이터 세트에서 이상치일 가능성이 높다고 간주된다. 이런 값들은 나머지 데이터와 상당히 다르기 때문에 특별한 주의가 필요하다.
Z-score 값이 -3 이하 또는 3 이상인 지역은 이상치로 간주되며, 붉은색으로 표시되어 있다.
•
-2와 2 사이의 값들은 이상하지 않은(normal) 범위로 간주되며, 노란색으로 표시되어 있습니다.
•
-2와 -3 사이, 2와 3 사이의 값들은 다소 이상하다고 여겨지는(moderately unusual) 범위로, 주황색으로 표시되어 있습니다.
Z-score 로 이상치 처리하기
1.
수동으로 계산하고, 제거하기
데이터 세트의 평균과 표준편차를 계산해 Z-score를 수동으로 계산한 뒤 임곗값을 넘는 데이터를 이상치로 처리하고 제거하기
2.
Scipy를 이용해 계산하고 제거하기
Scipy 라이브러리의 stats 모듈은 z-score계산을 자동화하는 함수를 제공.
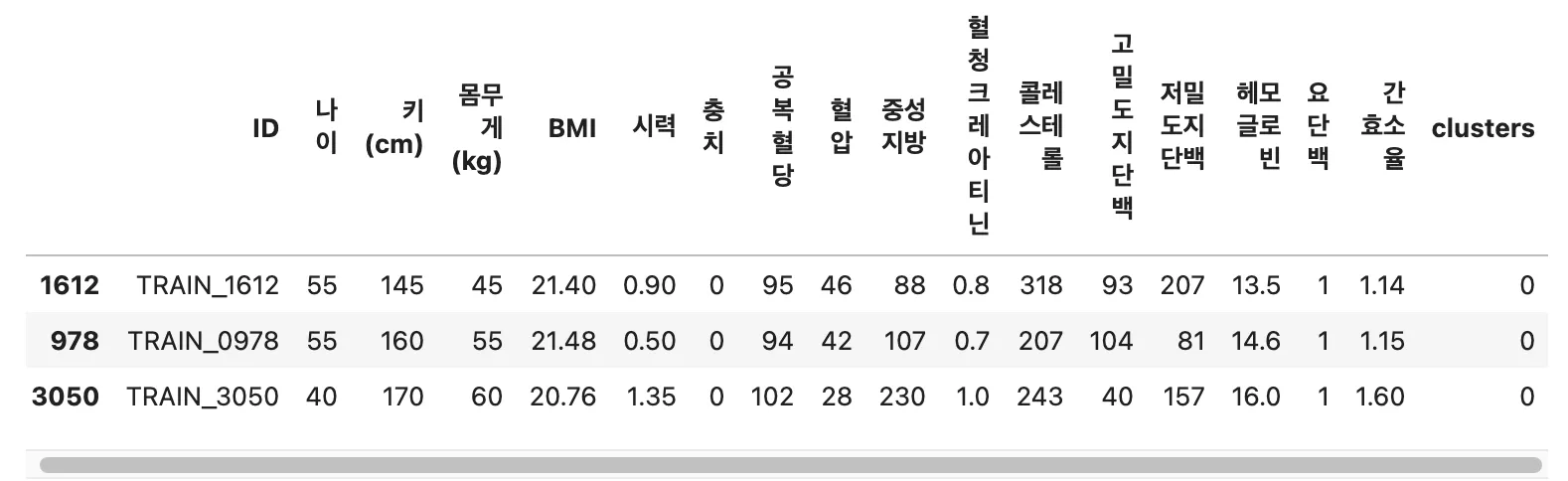
데이콘 중고차 데이터셋으로 실습하기
1.
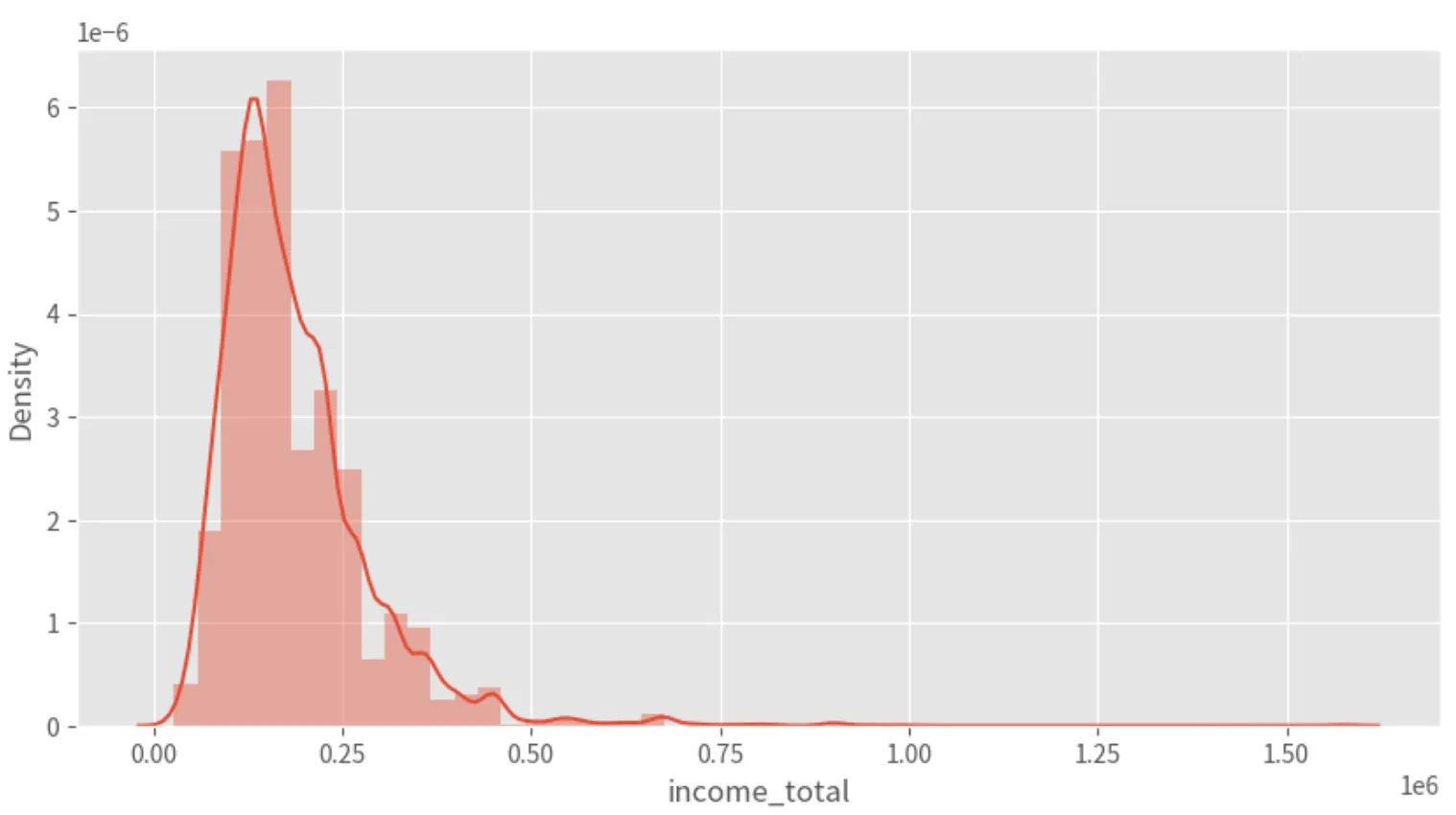
income_total 피처 분포 확인하기
plt.figure(figsize=(10,5))
sns.distplot(X_train['income_total'])
plt.show()
Python
복사
2.
income_total 이상치 개수 확인하기
•
Z-score 계산하는 함수 직접 만들기
def out_zscore(data, threshold=3):
mean = np.mean(data)
std = np.std(data)
zscores = [(x - mean) / std for x in data]
outliers = [x for x in data if np.abs((x - mean) / std) > threshold]
return zscores, len(outliers)
_, num_outliers = out_zscore(X_train.income_total)
print('Total number of outliers are", num_outliers)
Python
복사
결과 : Total number of outliers are 151
평균으로부터 +=3 표준편차 이상 떨어진 이상치가 151개 존재
•
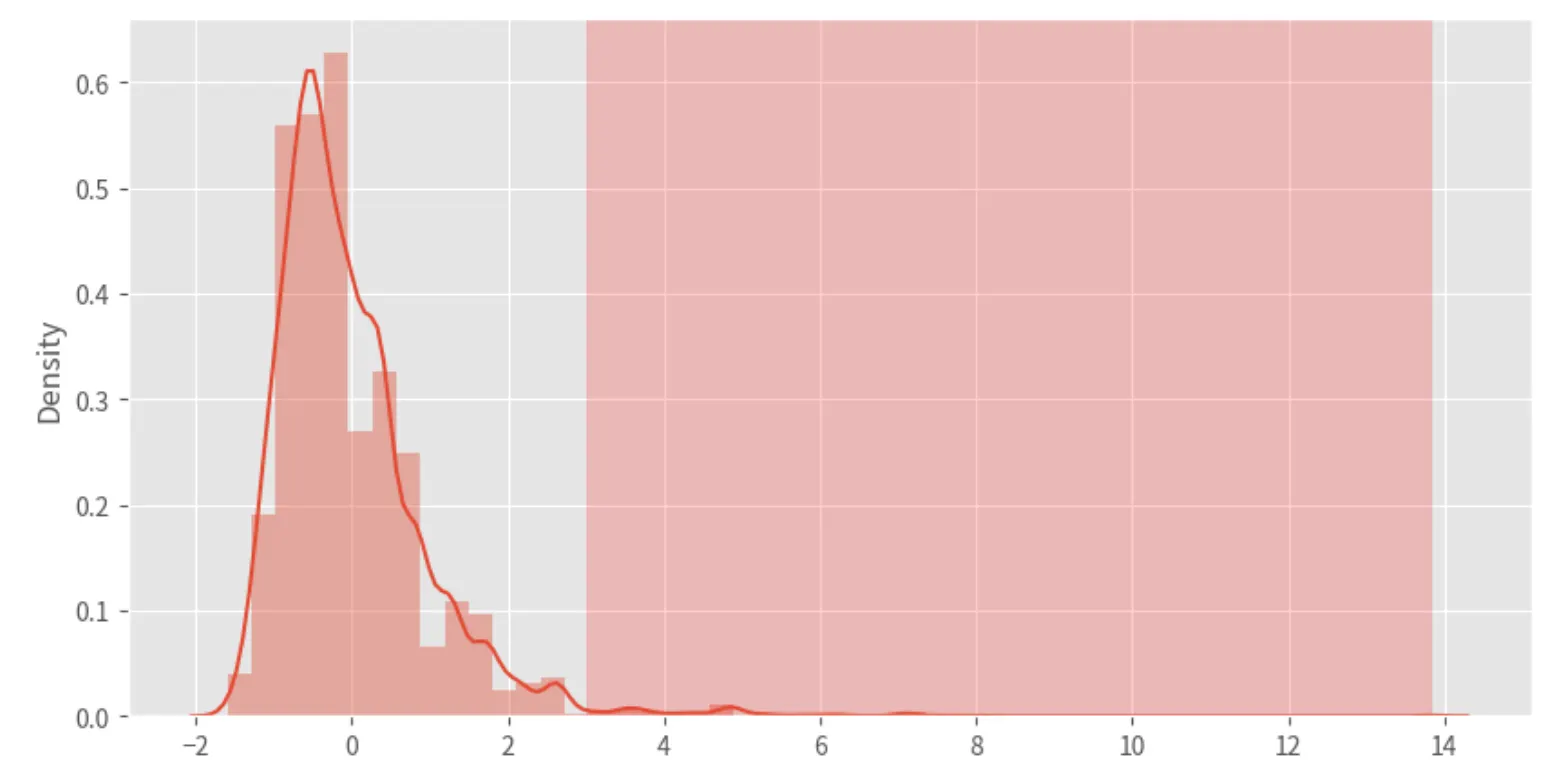
Z-score 분포 그려보기 (distplot) : KDE분포함수
zscores, _ = out_zscore(X_train.income_total)
plt.figure(figsize=(10,5))
sns.distplot(zscores)
plt.axvspan(xmin=3, xmax=max(zscores), alpha=0.2, color='red')
plt.show()
Python
복사
plt.axvspan 함수를 이용해서 데이터값이 3이상인 공간을 투명도 0.2인 빨간색으로 칠해줬다.
: 수직 영역을 강조할 때 사용됨.
•
임곗값 3을 넘는 이상치들 수동으로 제거해주기
Z_train = X_train.copy()
# Train 데이터의 평균, 표준편차 계산
mean_train = Z_train['income_total'].mean()
std_train = Z_train['income_total'].std()
# 임계값 설정
threshold = 3
# Train 데이터로 Z-점수 계산 및 이상치 제거
Z_train['z_score_income'] = (Z_train['income_total'] - mean_train) / std_train
train_no_outliers = Z_train[Z_train['z_score_income'].abs() <= threshold]
train_no_outliers = train_no_outliers.drop('z_score_income', axis=1)
train_no_outliers.shape
Python
복사
결과 : (11050, 19)
이상치를 제거하고 11050개의 데이터가 남은 것을 확인했다.
•
Scipy 라이브러리를 이용한 z-score 계산과 이상치 제거
stats 모듈을 사용한다.
from scipy import stats
Z_scipy_train = X_train.copy()
# z-score 계산
Z_scipy_train['z_score_income'] = stats.zscore(Z_scipy_train['income_total']
# 임곗값 설정
threshold = 3
# 임곗값을 기준으로 이상치 제거
train_no_outliers = Z_scipy_train[Z_scipy_train['z_score_income'].abs() <= threshold]
# z_score_income 컬럼 제거
train_no_outliers = train_no_outliers.drop('z_score_income', axis=1)
train_no_outliers.shape
Python
복사
stats 모듈의 zscore 함수를 사용한다.
결과 : (11050, 19)
Z-score 의 장단점
•
장점
◦
간단하고 직관적
◦
표준화된 형태로 표현되 서로 다른 데이터셋이나 변수 간 비교가 용이
◦
데이터가 정규 분포를 따를 경우, 매우 효과적
•
단점
◦
데이터의 분포가 비대칭이거나 긴 꼬리를 가진 형태일 경우, 오류가 발생할 수 있음
◦
이상치가 있을 경우, 평균과 표준편차에 영향을 미쳐 z-score계산에도 영향을 미침
◦
데이터에 이상치가 많을 경우, 효과적이지 못할 수 있음
◦
임곗값 설정이 주관적이며 이에 따라 결과가 달라질 수 있음
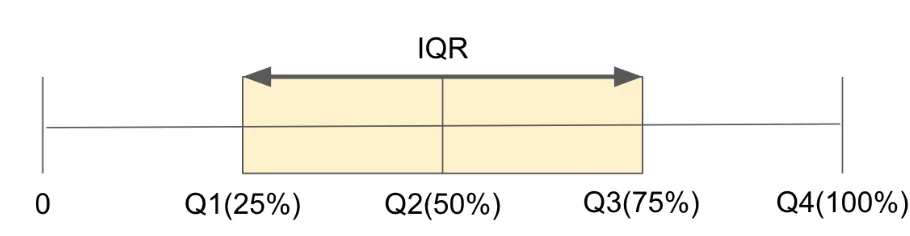
3.2.IQR로 이상치 처리하기
IQR은 데이터 세트의 중간 50% 범위를 측정하는 통계적 방법임.
IQR은 제 1사분위수(25%)와 제 3사분위수(75%) 사이의 차이로 정의됨
중앙값에 대한 분산을 나타내며, 이상치 탐지에 매우 유용
IQR = Q3 - Q1
이상치 하한 경계는 Q1 - 1.5 * IQR, 상한 경계는 Q3 + 1.5 * IQR
위의 경계를 벗어나는 데이터를 일반적으로 이상치로 간주한다.
•
Quantile 함수로 IQR 이상치 제거하기
pandas 라이브러리의 quantile 함수를 이용해 Q1, Q3 를 구하고 IQR를 계산할 수 있다.
•
Percentile 함수로 IQR 이상치 제거하기
Numpy 라이브러리의 percentile 함수를 이용해 백분위수를 구하고, IQR을 계산할 수 있다.
•
상자 그림 : Boxplot
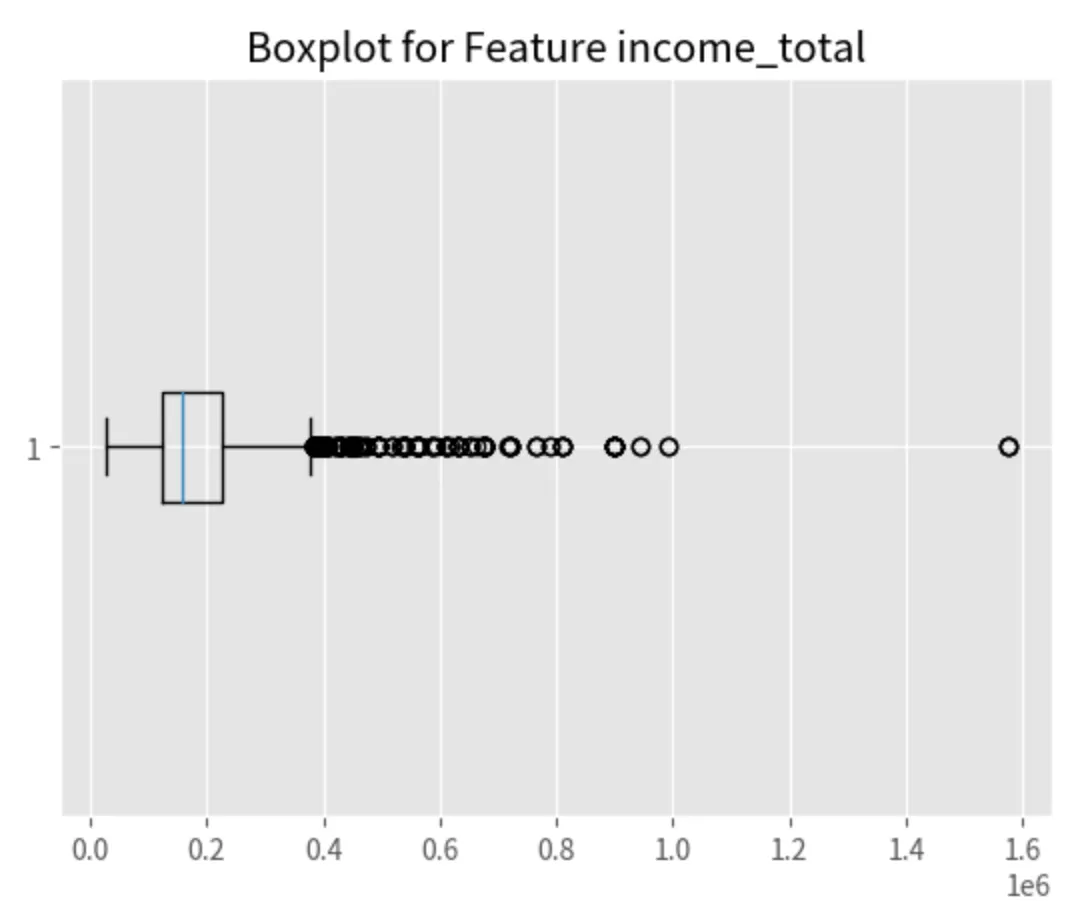
plt.boxplot(X_train['income_total'], vert=False) # vert=False 는 상자그림을 가로로
plt.title('Boxplot for Feature income_total')
plt.show()
Python
복사
IQR로 특성값의 이상치 개수를 계산하는 함수 만들기
1.
quantile 함수 (pandas)
def out_iqr(data):
Q1 = data.quantile(0.25)
Q3 = data.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5*IQR
upper_bound = Q3 + 1.5*IQR
return lower_bound, upper_bound
lower_bound, upper_bound = out_iqr(X_train['income_total'])
lower_outliers = X_train[X_train['income_total'] < lower_bound]
upper_outliers = X_train[X_train['income_total'] > upper_bound]
# 이상치 개수 세기
num_lower_outliers = len(lower_outliers)
num_upper_outliers = len(upper_outliers)
print("Number of lower outliers in 'income_total' column:", num_lower_outliers)
print("Number of upper outliers in 'income_total' column:", num_upper_outliers)
Python
복사
Number of lower outliers in 'income_total' column: 0
Number of upper outliers in 'income_total' column: 467
하위 이상치는 발견되지 않았고, 상위 이상치가 467개라는 것을 확인
이상치 제거하기
lower_bound, upper_bound = out_iqr(X_train['income_total'])
train_no_outliers_iqr = X_train[(X_train['income_total'] >= lower_bound) & (X_train['income_total'] <= upper_bound)]
print("Shape of train data after removing outliers using IQR:", train_no_outliers_iqr.shape)
Python
복사
Shape of train data after removing outliers using IQR: (10734, 19)
2.
percentile 함수 (numpy)
import numpy as np
Q1 = np.percentile(X_train['income_total'],25)
Q3 = np.percentile(X_train['income_total'],75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5*IQR
upper_bound = Q3 + 1.5*IQR
train_no_outliers_iqr_np = X_train[(X_train['income_total'] >= lower_bound)&(X_train['income_total'] <= upper_bound)]
print("Shape of train data after removing outliers using NumPy's percentile:", train_no_outliers_iqr_np.shape)
Python
복사
이상치 제거한 뒤, boxplot
plt.boxplot(train_no_outliers_iqr['income_total'], vert=False)
plt.title('Boxplot for Feature income_total')
plt.show()
Python
복사
IQR 의 장단점
•
장점
◦
극단치에 덜 예민하다 → 데이터의 분포가 비대칭일 때 유용
◦
직관적
◦
비모수적 접근 가능 → 즉, 정규 분포를 따르지 않아도 사용 가능하기 때문에 실제 상황에 더 유용
•
단점
◦
이상치를 정의하는 임곗값 (1.5*IQR)은 어느 정도 임의적임. 명확한 가이드라인이 없음
이상치를 꼭 제거해야 될까?
결과적으로 이상치는 꼭 제거해야 될 필요는 없다.
이상치를 다루는 다른 방법들이 고려되고 있다.
•
데이터 변환
로그 변환, 제곱근, 역수 취하기 등으로 분포를 바꿀 수 있음
•
이상치 점수화
이상치를 제거하지 않고, 이상치를 식별한 뒤 점수화한다. 모델링에 활용하거나 이상치 정도를 파악할 수 있음
•
이상치 치환
이상치를 다른 값으로 대체한다. 중앙값이나 평균값, 근삿값 등
•
모델 기반 접근
일부 머신 러닝 모델은 이상치를 알아서 처리한다. 랜덤 포레스트와 같은 트리 기반 모델은 이상치에 민감하지 않은 경우도 있다.
•
이상치를 고려한 모델링
오히려 이상치가 중요한 정보를 제공하는 경우에는 결과에 미치는 영향을 분석할 수 있다.
다변량 이상치 탐지
•
DBSCAN
데이터들을 그룹화해서 이상치를 식별하는데 사용되는 클러스터링 알고리즘.
데이터 포인트의 밀도를 기반으로 주변 데이터 포인트와의 관계를 고려하여 이상치를 찾아냄.
다양한 데이터 구조에서 유용함.
•
LOF
데이터 포인트의 ‘지역적 밀도’를 측정하고, 이를 주변 포인트의 밀도와 비교해 이상치를 탐지.
데이터의 지역적 밀도가 다를 때 효과적.
DBSCAN 이용해서 이상치 탐지하기
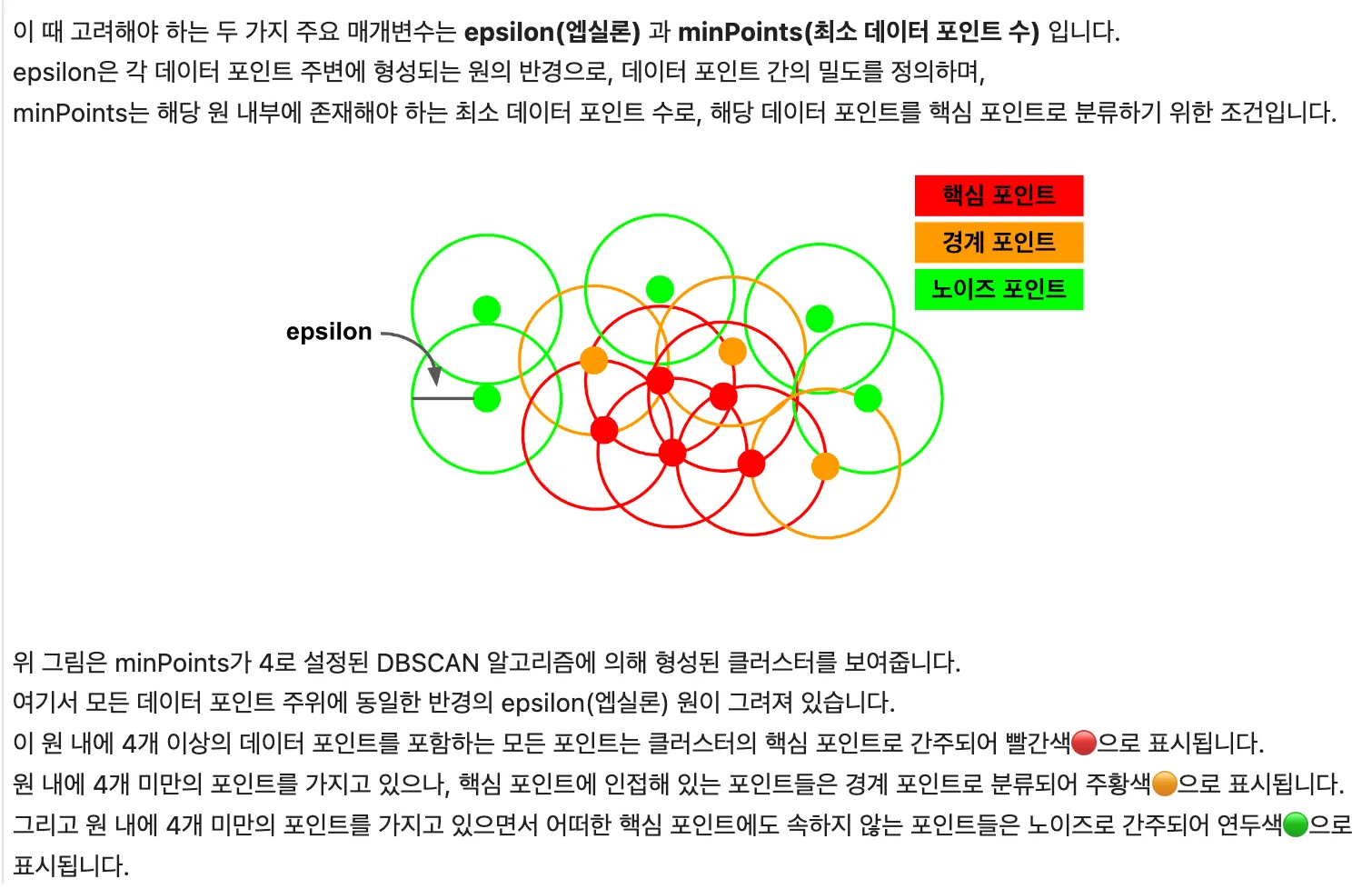
클러스터를 형성한 뒤, 여기에 속하지 않는 데이터들을 이상치로 간주하는 알고리즘
K-means 알고리즘의 대안으로 사용되며, 미리 클러스터의 개수를 정하지 않고 데이터 자체의 밀도에 기반해 클러스터링을 수행한다.
몇 가지 key point는
•
핵심 포인트
주변 지역(eps 거리 내)에 일정 수(min_samples) 이상의 이웃 포인트가 있는 데이터 포인트
이 포인트들은 클러스터링 과정에서 클러스터의 '핵심'을 형성
•
경계 포인트
핵심 포인트의 이웃이지만, 그 자체로는 핵심 포인트의 조건(즉, min_samples 이상의 이웃)을 충족하지 않는 포인트
클러스터의 ‘경계’를 형성
•
노이즈 포인트
핵심 포인트나 경계 포인트가 아닌 모든 포인트
데이터셋에서 ‘이상치’를 나타냄
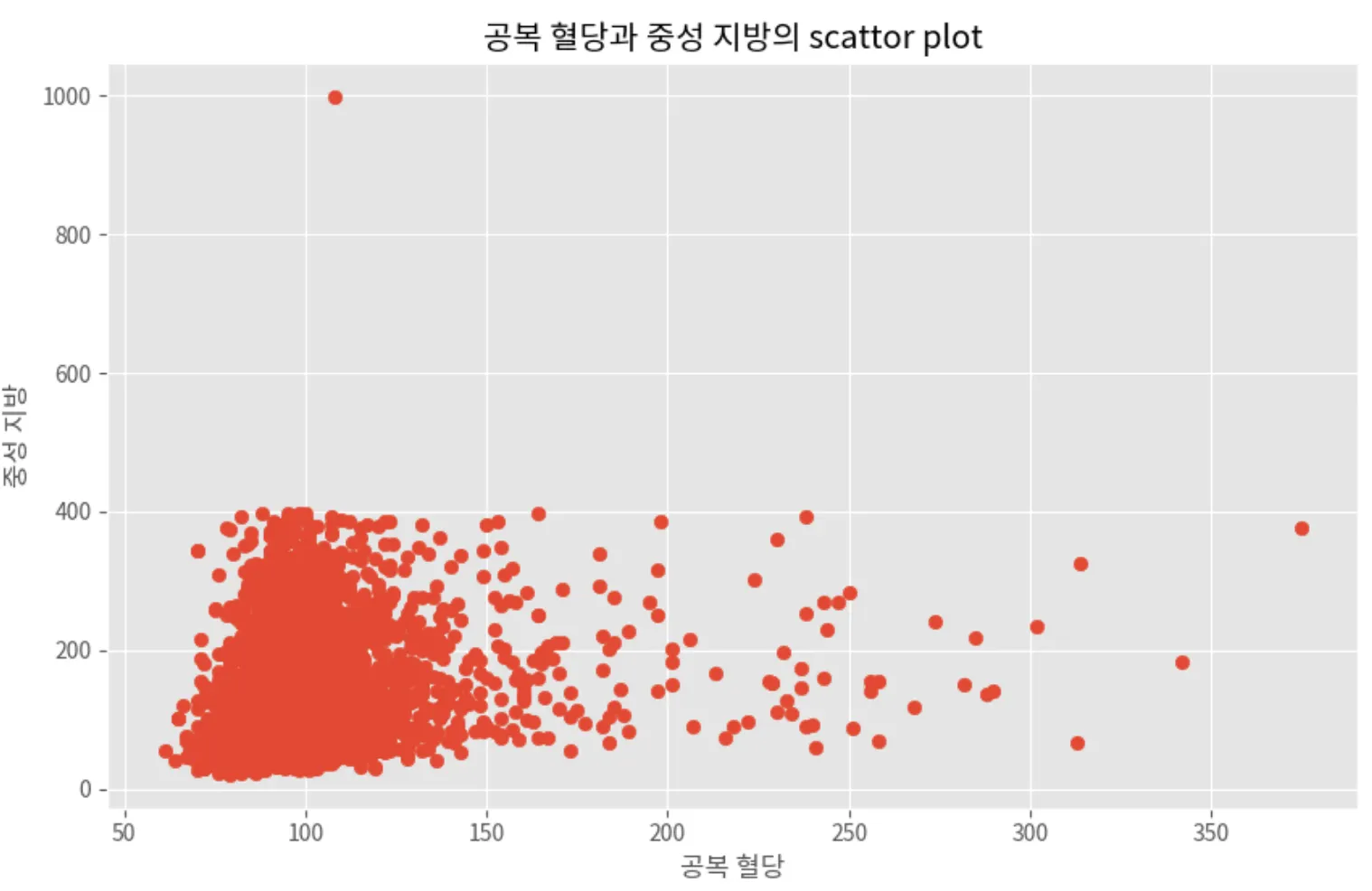
다변량 데이터들의 산점도 분석
ex) ‘공복 혈당’ 과 ‘중성 지방’ 두 변수의 산점도를 생성해서 관계를 시각화한다.
import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
plt.scatter(X_train['공복 혈당'], X_train['중성 지방'])
plt.title('공복 혈당과 중성 지방의 scattor plot')
plt.xlabel('공복 혈당')
plt.ylabel('중성 지방')
plt.grid(True)
plt.show()
Python
복사
DBSCAN으로 이상치 탐지하기
< 사전 작업 >
•
두 변수 표준화하기
•
DBSCAN 알고리즘 적용하기
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
DBSCAN_train = X_train.copy()
numeric_columns = ['공복 혈당','중성 지방']
data_numeric = DBSCAN_train[numeric_columns]
# 데이터 표준화
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data_numeric)
db = DBSCAN(eps=0.5, min_samples=5).fit(data_scaled) #eps : 입실론반경 , min_samples : 입실론 반경 최소 샘플 수
labels = db.lables_
pd.Series(labels).value_counts()
Python
복사
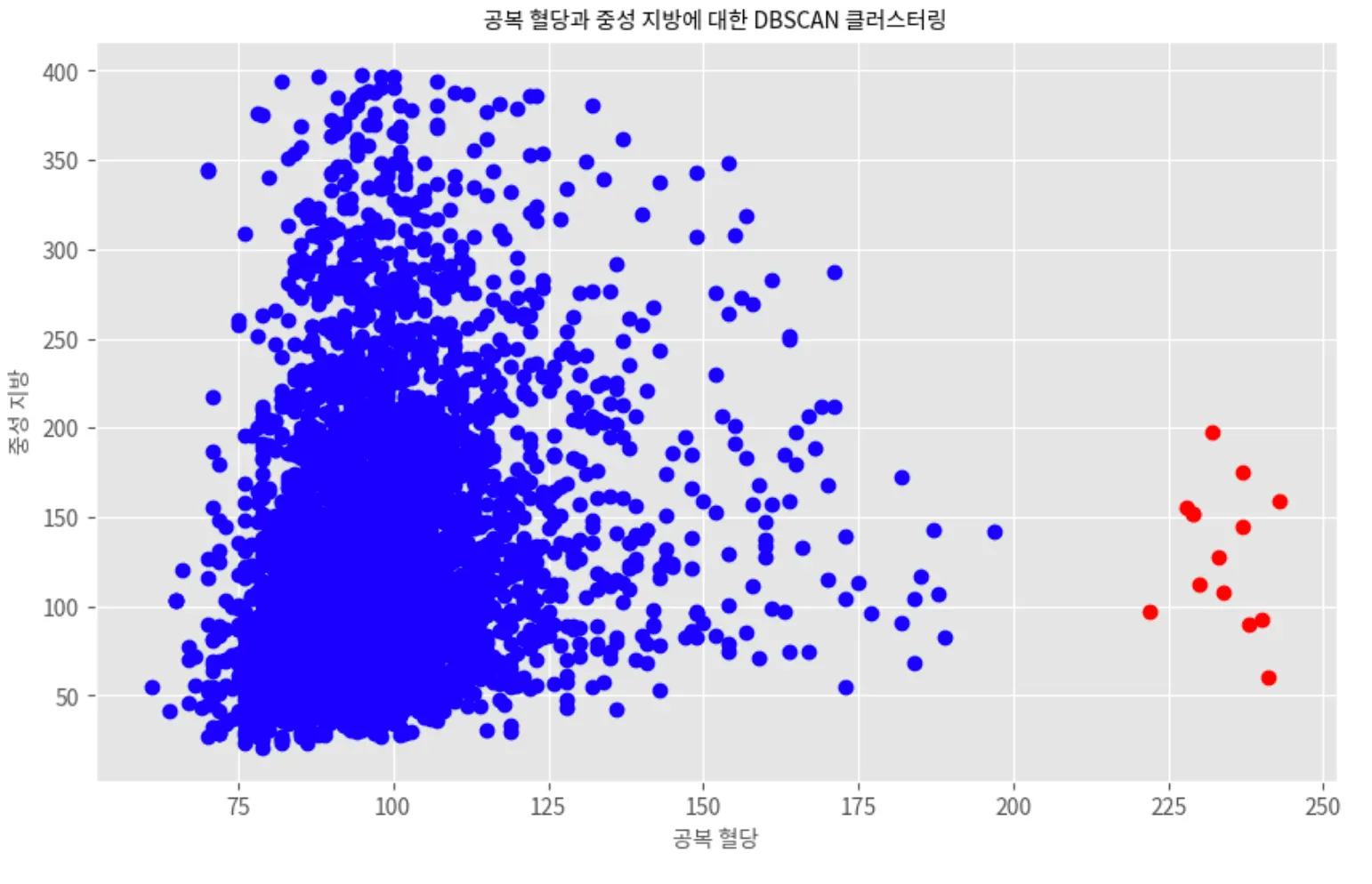
0 4839
-1 42
1 14
2 5
dtype: int64
Plain Text
복사
DBSCAN 알고리즘은 데이터 포인트에 클러스터 라벨을 할당한다.
-1 : 이상치
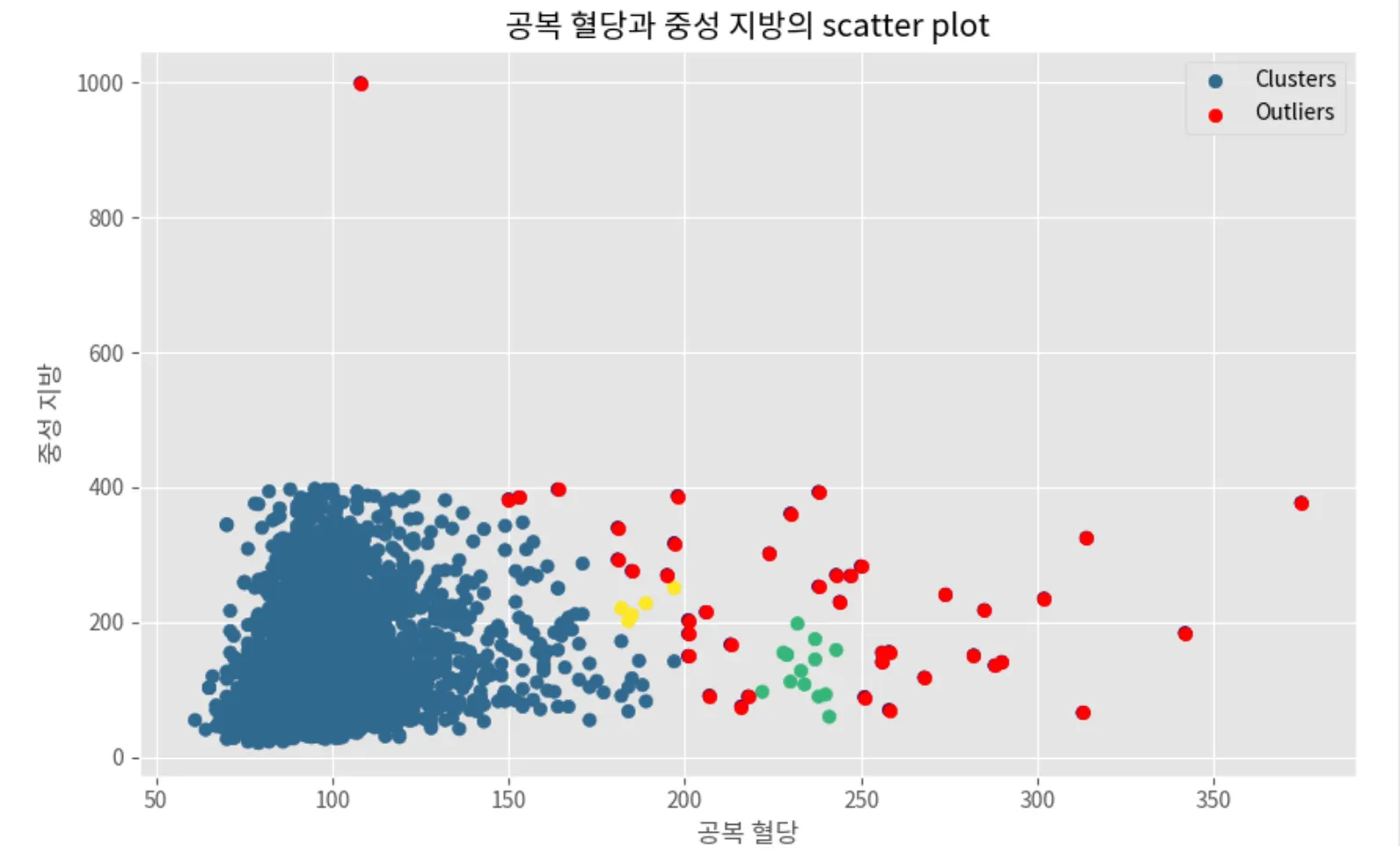
클러스터링 결과 시각화
plt.figure(figsize=(10,6))
unique_labels = set(labels)
color = ['blue','red']
for color, label in zip(color, unique_labels):
if label == -1:
# 이상치는 빨간색으로 표시
outlier_color = 'red'
else:
# 클러스터에 속한 데이터는 파란색으로 표시
cluster_color = 'blue'
sample_mask = labels == label
plt.plot(data_numeric.iloc[sample_mask,0], data_numeric.iloc[sample_mask,1], 'o', color=color)
# x축과 y축에 라벨 추가
plt.xlabel('공복 혈당', fontsize=10)
plt.ylabel('중성 지방', fontsize=10)
plt.title('공복 혈당과 중성 지방에 대한 DBSCAN 클러스터링', fontsize=10)
plt.grid(True)
plt.show()
Python
복사
이상치 제거 결과
•
클러스터 레이블 추가
•
이상치가 아닌 데이터 선택
clusters_sample = db.fit_predict(data_scaled)
DBSCAN_train['clusters'] = clusters_sample
sample_no_outliers = DBSCAN_train[DBSCAN_train['clusters']!= -1]
display(sample_no_outliers.head(3))
display(f"이상치가 아닌 데이터 포인트들의 수: {len(sample_no_outliers)}")
Python
복사
'이상치가 아닌 데이터 포인트들의 수: 4858'
plt.figure(figsize=(10,6))
plt.scatter(DBSCAN_train['공복 혈당'], DBSCAN_train['중성 지방'], c=DBSCAN_train['clusters'], cmap='viridis', label='Clusters') # cluster별로 데이터 찍기
plt.scatter(DBSCAN_train[DBSCAN_train['clusters'] == -1]['공복 혈당'],
DBSCAN_train[DBSCAN_train['clusters'] == -1]['중성 지방'],
color = 'red', label = 'Outliers') # 이상치 데이터 다시 찍기
plt.title('공복 혈당과 중성 지방의 scatter plot')
plt.xlabel('공복 혈당')
plt.ylabel('중성 지방')
plt.legend()
plt.grid(True)
plt.show()
Python
복사
DBSCAN 장단점
•
장점
◦
모델 가정 불필요
◦
클러스터 개수 설정 불필요
◦
이상치에 영향 안받음
◦
파라미터 설정으로 유연하게 조정
▪
eps , min_samples
•
단점
◦
파라미터 설정에 따라 결과가 달라져 여러 시도 필요
◦
변수 스케일에 영향, 사전 데이터 처리 필요
◦
차원의 저주로 고차원 데이터에서 성능이 저하될 수 있음
◦
밀도가 크게 변할 경우, 한가지 eps로 모든 클러스터를 식별하기 힘듦
◦
매우 다양한 크기의 클러스터가 존재할 경우, 모든 클러스터를 동일하게 잘 식별하지 못할 수 있음
LOF 를 활용해서 이상치 탐지하기
LOF(local outlier factor)는 주변 이웃과 비교해 데이터가 얼마나 이상한지를 평가하는 알고리즘
각 데이터들의 지역 밀도를 계산하고, 주변 이웃 데이터들의 밀도와 비교.
LOF 점수는 데이터 포인트가 주변 이웃과 얼마나 다른지를 나타냄. 값이 클수록 이상치일 가능성이 큼
•
이웃 개수 설정
고려할 이웃 데이터의 개수를 설정(n_neighbors) → 얼마나 지역적으로 데이터를 보는지 결정
•
지역 밀도 계산
가장 가까운 n_neighbors 이웃들까지의 거리의 평균을 계산.
•
LOF 점수 계산
점수가 1에 가까울 수록 이웃들과 비슷한 밀도를 가지고 있는 것.
1보다 높으면 높을수록 이상치 가능성이 높아짐
•
이상치 결정
LOF 값이 특정 임곗값 이상이면 이상치로 분류. 경험적으로 결정하거나 비율로 설정
LOF 알고리즘으로 이상치 판별하기
•
LocalOutlierFactor 알고리즘은 배열을 입력으로 받는다 → numpy 사용
from sklearn.neighbors import LocalOutlierFactor
# 데이터 준비
LOF_train = X_train.copy()
numeric_columns = ['공복 혈당', '중성 지방']
data_numeric = LOF_train[numeric_columns].values # 넘파이 배열로 변환
# Local Outlier Factor 모델 생성
clf = LocalOutlierFactor(n_neighbors=50, contamination='auto') #이웃수:50, contamination:이상치의 비율 설정 -> 'auto':자동으로 비율 추정
# 이상치 탐지
labels = clf.fit_predict(data_numeric) # 학습과 예측 레이블의 결과
pd.Series(labels).value_counts()
Python
복사
1 4781
-1 119
dtype: int64
Plain Text
복사
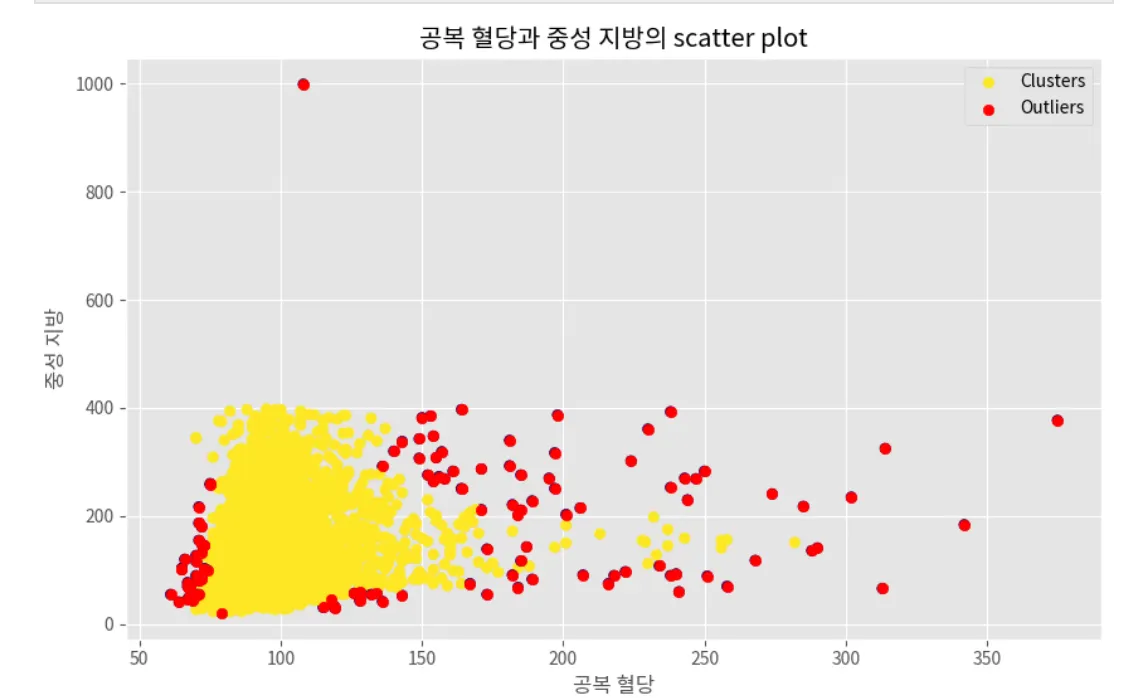
정상 데이터 포인트는 1, 이상치 데이터 포인트는 -1로 레이블됨.
119개의 데이터 포인트가 이상치로 분류되었고, 주변 이웃에 비해 상대적으로 낮은 밀도를 갖고 있는 것으로 판단됨.
이상치 데이터 필터링하기
LOF_train['outliers_lof'] = labels
sample_no_outliers = LOF_train[LOF_train['outliers_lof'] != -1]
display(sample_no_outliers.head(3))
display(f"이상치가 아닌 데이터 포인트들의 수: {len(sample_no_outliers)}")
Python
복사
'이상치가 아닌 데이터 포인트들의 수: 4781'
LOF 를 이용한 이상치 시각화
plt.figure(figsize=(10, 6))
plt.scatter(LOF_train['공복 혈당'], LOF_train['중성 지방'], c=LOF_train['outliers_lof'], cmap='viridis', label='Clusters')
plt.scatter(LOF_train[LOF_train['outliers_lof'] == -1]['공복 혈당'],
LOF_train[LOF_train['outliers_lof'] == -1]['중성 지방'],
color='red', label='Outliers')
plt.title('공복 혈당과 중성 지방의 scatter plot')
plt.xlabel('공복 혈당')
plt.ylabel('중성 지방')
plt.legend()
plt.grid(True)
plt.show()
Python
복사
LOF 장단점
•
장점
◦
지역적 관점에서 이상치를 식별하기 때문에 밀도에 영향을 받지 않음
◦
다양한 데이터셋에 적용 가능. 밀도가 불균형한 데이터셋에서도 유용함
◦
이상치의 순위화 : 이상치로 판단되는 정도를 수치로 제공.
◦
파라미터 조정의 유연성 : 이웃의 수를 조정해서 모델의 민감도를 조절할 수 있음
•
단점
◦
파라미터 조정의 어려움 : 파라미터 조정에 따라 정확도가 달라지기 때문에 경험치가 필요함
◦
고차원 데이터의 한계 : 차원의 저주에 영향을 받을 수 있음
◦
계산 복잡성 : 큰 데이터셋의 경우, 데이터 포인트의 이웃을 찾는 과정이 복잡할 수 있음
◦
스케일링 필수
특정 변수의 데이터 분포가 한쪽으로 심하게 치우쳐져 있는 문제가 생길 경우 데이터 분석을 하기 앞서 정비해줄 필요가 있다.
방식에는 여러가지가 있는데, 다음과 같다.
threshold 를 정해서 데이터 잘라내기
1) 양쪽 사이드에서 몇 %를 제거해내는 방법
min_threshold, max_threshold = df['var'].quantile([0.01,0.99]) # 양쪽 사이드 1% 에 해당하는 값
# 위의 범위 사이에 존재하는 데이터들만 뽑아내기
df[(bnb['var'] > min_threshold)&(bnb['var'] < max_threshold)]
SQL
복사