def recusion(num):
if num > 0:
print('*' * num)
return recusion(num - 1)
else:
return 1
recusion(10)
########### 결과 ###########
**********
*********
********
*******
******
*****
****
***
**
*
Python
복사
def factorial(num):
if num > 0:
return num * factorial(num - 1)
else:
return 1
print(factorial(10))
########## 결과 ###########
3628800
Python
복사
# 재귀 알고리즘을 이용해서 최대 공약수 계산
# 유클리드 호제법을 활용하자 : n1, n2, n1 % n2 가 있다고 할 때, n1과 n2의 최대공약수는 n2와 n1 % n2 의 최대공약수와 같다
# 이때, n1 > n2 여야하고 n1 % n2 값이 0이 되면 멈춘다
def gcd(n1,n2):
if n1 % n2 == 0: #나머지가 0이 되면 n2를 반환 -> 최대공약수
return n2
else:
return gcd(n2, n1 % n2)
print(f' gcd(82,32) : {gcd(82,32)}')
print(f' gcd(96,40) : {gcd(96,40)}')
############## 결과 ###############
gcd(82,32) : 2
gcd(96,40) : 8
Python
복사
# 일반적인 반복문 이용해서 최대공약수 구하기
def gcd(n1,n2):
maxCommon = 0
for i in range(1,(n1 + 1)): # n1이 더 크다고 할때,
if n1 % i == 0 and n2 % i == 0:
maxCommon = i
return maxCommon
print(f' gcd(82,32) : {gcd(82,32)}')
print(f' gcd(96,40) : {gcd(96,40)}')
Python
복사
하노이의 탑
알고리즘 문제에서 많이 출제되는 방법이다.
재귀 함수를 이용해서 가장 큰 원판을 옮겨 놓고 나머지 원판들은 또 다른 탑이 되어 쌓아나가는 형식이다.
해당 게임의 원리는 크게 세 가지 알고리즘으로 구분할 수 있다.
1.
마지막 원판을 제외한 모든 원판을 경유지 기둥으로 위치시키는 알고리즘 → 재귀 함수 필요
2.
마지막 원판을 도착 기둥으로 위치시키는 알고리즘
3.
경유지 기둥에 있는 모든 원판을 도착 기둥으로 위치시키는 알고리즘 → 재귀 함수 필요(원판 옮기기의 반복)
# 하노이 탑
def moveDisc(discCnt, fromBar, toBar, viaBar): #원판의 개수, 시작 기둥, 목표 기둥, 경유 기둥
if discCnt == 1: # 맨 위에 있는 원판을 목표기둥에 옮기는 과정
print(f'{discCnt}원판을 {fromBar}에서 {toBar}로 이동!')
else:
moveDisc(discCnt-1, fromBar, viaBar, toBar) # (discCnt - 1)개의 원판을 경유 기둥으로 보내는 알고리즘
# discCnt 를 목적(경유가 될 수도 있음) 기둥으로 이동
print(f'{discCnt}원판을 {fromBar}에서 {toBar}로 이동!')
moveDisc(discCnt - 1, viaBar, toBar, fromBar)
moveDisc(3,1,3,2)
Python
복사
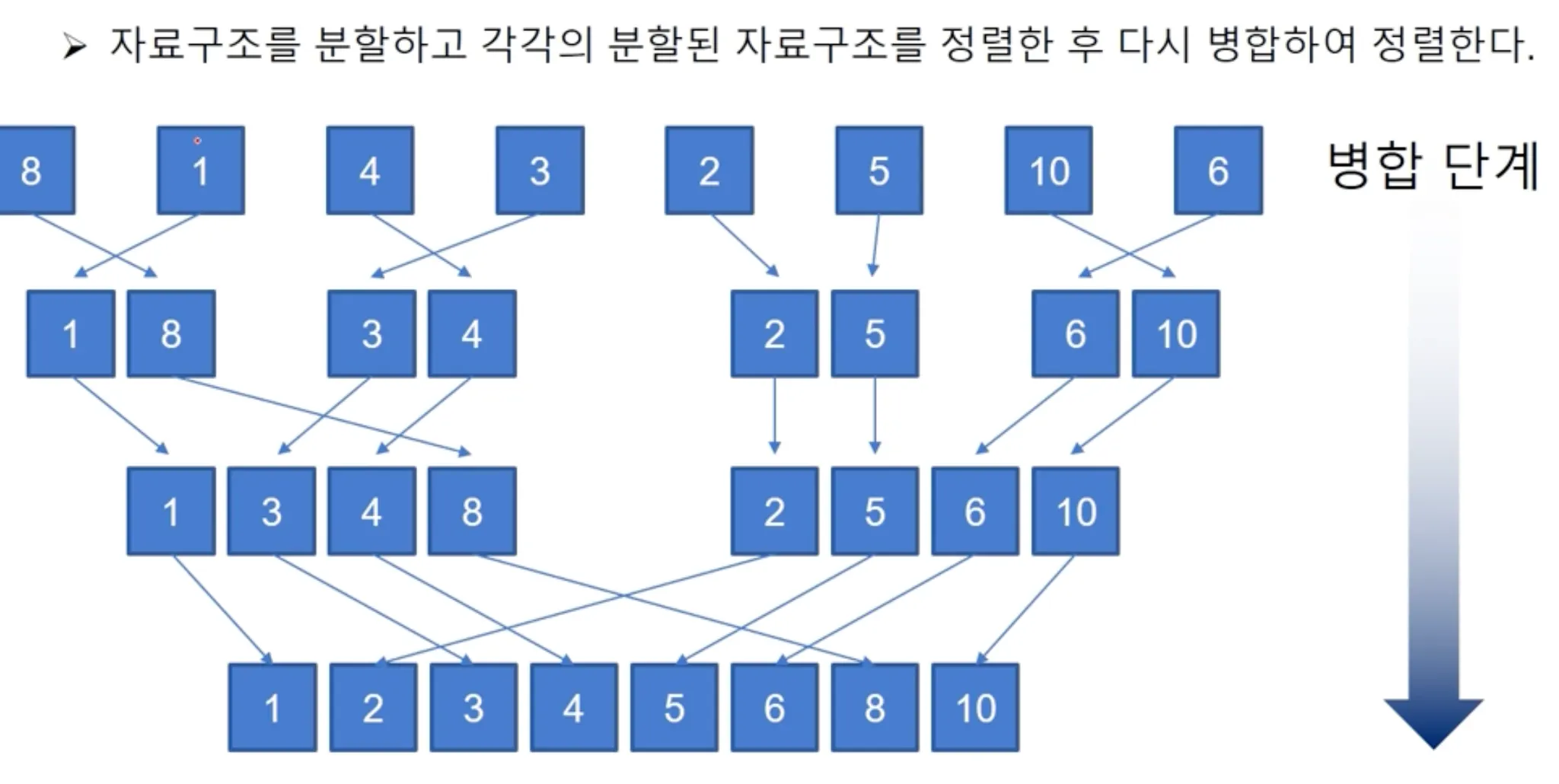
병합 정렬 → 다시!!!
자료 구조를 분할하고 각각의 분할된 자료구조를 정렬한 후 다시 병합하여 정렬하는 방법
앞서 공부한 삽입, 버블 정렬보다는 속도면에서 향상된 알고리즘이다.
def mSort(ns):
# 원소들을 쪼개는데, 개수가 2보다 작아지면 return 한다 -> 원소 하나씩 담기게 되니까
if len(ns) < 2:
return ns
# 쪼개지는 기준이 절반으로 쪼개니까, 절반에 해당하는 Index를 설정해주자
midIdx = len(ns) // 2 # 2로 나눈 몫이 절반에 해당하는 index다.
# 쪼개진 양쪽의 데이터에 대해서 다시 나누는 과정 재귀적으로 반복
leftNums = mSort(ns[:midIdx])
rightNums = mSort(ns[midIdx:])
print(leftNums)
print(rightNums)
print(ns)
# 다 쪼개졌으면 병합하는 단계
mergeNums = []
leftIdx = 0; rightIdx = 0
while leftIdx < len(leftNums) and rightIdx < len(rightNums):
if leftNums[leftIdx] < rightNums[rightIdx]:
mergeNums.append(leftNums[leftIdx])
leftIdx += 1
else:
mergeNums.append(rightNums[rightIdx])
rightIdx += 1
mergeNums = mergeNums + leftNums[leftIdx:]
mergeNums = mergeNums + rightNums[rightIdx:]
return mergeNums
nums = [8,1,4,3,2,5,10,6]
print(f'sorted number : {mSort(nums)}')
Python
복사
Python
복사
퀵정렬
기준 값보다 작은 값과 큰 값으로 분리한 후 다시 합치는 방법
이 기준값을 pivot 이라고 부르는데, 이 값을 어떤 값으로 잡느냐에 따라서 성능이 NlogN ≤ BiG O ≤ N^2 으로 달라질 수 있다.
ex ) 이미 정렬이 되어 있는 경우에는 최악의 시간 복잡도인 N^2 이 될 수도 있다.
def qsort(ns): # 들어올 숫자의 배열값
if len(ns) < 2:
return ns
midIdx = len(ns) // 2 # 중간값을 pivot 으로 설정, index 저장
midVal = ns[midIdx] # 중간값 저장
smallNums = []; sameNums = []; bigNums = [] # pivot 값보다 작은 값, 동일한 값, 큰 값을 넣어줄 리스트 지정
# 각각의 원소들을 smallNums, sameNums, bigNums 에 할당하는 과정
for n in ns:
if n < midVal:
smallNums.append(n)
elif n == midVal:
sameNums.append(n)
else:
bigNums.append(n)
return qsort(smallNums) + sameNums + qsort(bigNums)
nums = [8,1,4,3,2,5,4,10,6,8]
print(f'qsort(nums) : {qsort(nums)}')
Python
복사
def quickNums(ns, asc=True):
if len(ns) < 2:
return ns
midIdx = len(ns) // 2
midVal = ns[midIdx]
smallNums = []; sameNums = []; bigNums = []
for n in ns:
if n < midVal:
smallNums.append(n)
elif n == midVal:
sameNums.append(n)
else:
bigNums.append(n)
if asc: # 오름차순 경우
return quickNums(smallNums) + sameNums + quickNums(bigNums)
else: # 내림차순 경우, 재귀함수 내에서도 설정해줘야 된다.
return quickNums(bigNums,False) + sameNums + quickNums(smallNums,False)
Python
복사
import random
import quick
rNums = random.sample(range(1,100),10)
print(f'not sorted nums : {rNums}')
sortedNums = quick.quickNums(rNums) # 오름차순 정렬
print(f'quick sorted nums : {sortedNums}')
sortedNumsDesc = quick.quickNums(rNums,False) # 내림차순 정렬
print(f'quick descending sorted Nums : {sortedNumsDesc}')
Python
복사
실행 파일에서 값을 넣어준다고 재귀함수에도 반영되는 것은 아니다! 이를 유의해서 사용하자
sales = [12000, 13000, 12500, 11000, 10500, 98000, 91000, 91500, 10500, 11500,
12000, 12500]
def salesUpandDown(s):
if len(s) == 1:
return s
print(f'sales : {s}')
verseSales = s.pop(0) # 첫 인덱스 제거해서 저장
currentSales = s[0] # 기준이 되는 매출
increase = currentSales - verseSales
if increase > 0:
increase = '+' + str(increase)
print(f'매출 증감액: {increase}')
return salesUpandDown(s)
if __name__ == '__main__':
salesUpandDown(sales)
Python
복사
# mode.py
class NumsSum:
def __init__(self,n1,n2):
self.bigNum = 0 # 들어온 수 중 더 큰수를 지정할 변수
self.smallNum = 0 # 들어온 수 중 작은 수를 지정할 변수
self.setN1N2(n1,n2)
def setN1N2(self,n1,n2): # 큰 수와 작은 수를 지정해줄 함수
self.bigNum = n1
self.smallNum = n2
if n1 < n2:
self.bigNum = n2
self.smallNum = n1
# 큰 수 이전까지의 합 - 작은 수까지의 합 = 구하고자 하는 값
def addNum(self, n): # 지정한 숫자까지의 합을 구해주는 함수
if n <= 1:
return n
return n + self.addNum(n-1)
def sumBetweenNums(self):
return self.addNum(self.bigNum - 1) - self.addNum(self.smallNum)
Python
복사
# 사용자가 정수 2개를 입력하면 작은 정수와 큰 정수 사이의 모든 합을 구하는 재귀 프로그램을
# 만들자.
import mode
n1 = int(input('input number1 : '))
n2 = int(input('input number2 : '))
ns = mode.NumsSum(n1,n2)
result = ns.sumBetweenNums()
print(f'result :{result}')
Python
복사