차원 축소

차원의 저주

1. 주성분 분석(PCA, 비지도 학습)

특징

방식

2. Sklearn 의 PCA

PCA 의 장단점

2. LDA - 선형 판별 분석(지도 학습)

Screeplot - 최적의 차원 수 찾아내기

LDA와 PCA 변환 데이터의 3D 시각화

4. incremental PCA (IPCA)

5. kernal PCA

차원의 저주

기본적인 머신 러닝 모델에서는 특성(변수)들이 전체 데이터에 비해 상대적으로 많게 되면, 모델의 성능이 떨어지게 된다. 이를 두고 차원의 저주 라고 부른다.

때문에 이를 해결하기 위한 방법으로 원본 데이터의 핵심 정보와 패턴을 유지하면서 더 낮은 차원의 공간으로 표현할 수 있는 차원 축소 방법 이 도입되었다.

차원 축소는 데이터의 중요한 특성을 보다 명확하게 드러낸다는 점에서 더 효과적인 인사이트와 결론 을 내리는 데도 도움이 된다.

1. 주성분 분석(PCA, 비지도 학습)

특징

•

차원 수(피처 수)를 줄이는 대표적인 방법

•

고차원의 특징(분산)을 최대한 유지하는 방식으로 차원 축소 진행

•

선형 방법을 사용한다.

•

기존 Feature 수만큼 추출 가능하다.

방식

주성분 분석을 수행할 때 주로 2가지 방법으로 진행한다.

•

고윳값 및 고유벡터를 사용하는 방법 → 고윳값 분해

•

SVD를 사용하는 방법 → 특이값 분해

하지만, 우리가 사용할 사이킷런에서는 특이값 분해(SVD)를 이용해 계산하는데, 그 이유는 다음과 같다.

고윳값 분해에 비해 수치적으로 더 안정적이다. 특히, 고차원 데이터나 특이값이 매우 작은 경우에 이점이 있다.

고차원 데이터에 대해서 효율적으로 작동하며, 분산이 낮은 주성분을 빠르게 제거할 수 있다.

원본 데이터셋 X에 대한 SVD는 다음과 같이 나타낸다.

X = U\sum V^{T}

•

U = m X m 직교행렬 → XXTXX^TXXT 의 eigenvector

◦

PCA에서 주성분을 추출하는 데 직접적으로 사용되지 않음

◦

데이터의 행과 관련된 변환

•

V = n X n 직교행렬 → XTXX^TXXTX 의 eigenvector, PCA의 주성분행렬

◦

원본 데이터의 특성(열)에 대한 정보를 담고 있는 오른쪽 특이 벡터들

◦

각 행은 원본 데이터의 특성들의 선형 결합으로 이루어진 새로운 축(주성분)을 나타내며, 이는 데이터의 중요한 변동성을 포착

•

∑ \sum ∑ = m X n 대각행렬 → XXTXX^TXXT 또는 XTXX^TXXTX 의 eigenvector의 제곱근을 대각원소로 하는 행렬

◦

PCA에서 주성분을 추출하는 데 직접적으로 사용되지 않음

◦

분산의 크기를 나타냄

< 예제 데이터 활용해서 pca 구하기 >

np.random.seed(4)
m = 60
w1, w2 = 0.1, 0.3
noise = 0.1

angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
X = np.empty((m,3))
X[:,0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
X[:,1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
X[:,2] = X[:,0] * w1 + X[:,1] * w2 + noise * np.random.randn(m)

print('X shape: ', X.shape)
Python
복사

1) eigen - decomposition(고윳값 분해)을 이용한 pca 구하기

먼저, 공분산 행렬을 구해야 한다.

X_cen = X - X.mean(axis=0) # 평균을 0으로
X_cov = np.dot(X_cen.T,X_cen) / 59
print(X_cov) # 공분산 행렬

# 물론, np.cov()를 이용해서 구할 수도 있다.
# print(np.cov(X_cen.T))
Python
복사

위에서 구한 공분산 행렬 X_cov 에 대해 np.linalg.eig 를 이용해 eigenvalue(w)와 eigenvector(v) 를 구할 수 있다.

w, v = np.linalg.eig(X_cov)

print('eigenvalue :', w)
print('eigenvector :\n',v)

print('explained variance ratio :', w / w.sum()) 
Python
복사

2) SVD(특이값 분해)를 이용한 PCA 구하기

np.linalg.svd를 이용하여 SVD를 구하기

# 주성분에는 V_t만 사용 : 열에 대한 정보가 담긴 정방행렬
U, D, V_t = np.linalg.svd(X_cen)

print('singular value :', D)
print('singular vector :\n', V_t.T)

print('explained variance ratio :', D**2 / np.sum(D**2))

# 주성분 개수 설정
n_components = 3

# n_components에 해당하는 주성분만 선택
components_train = V_t[:n_components]

components_train.shape
Python
복사

2. Sklearn 의 PCA

PCA(n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None) 
Python
복사

•

n_components : 원하는 주성분 개수를 지정

◦

int로 설정 → 개수만큼 주성분 생성

◦

float로 설정 → 분산 설명 비율을 기준으로 주성분 개수를 자동으로 생성

ex) 0.95 → 데이터의 95% 분산을 설명하는 최소한의 주성분 개수를 선택

◦

None → 데이터의 모든 주성분 반환

•

copy : 데이터 복사 여부 설정 

◦

True → (default) 데이터를 복사해서 PCA수행, 원본 데이터 변경 X

◦

False → 원본 데이터에 직접 적용 → 변형됨

•

whiten : PCA 결과 정규화 여부 설정 → 주성분을 독립적이고 동일한 분산을 가지도록 만들기 때문에 일부 머신러닝 알고리즘에서 성능 향상에 도움이 될 수 있음

◦

False → (default) PCA 결과를 정규화해서 각 주성분의 분산이 1이 되도록 변형

◦

True : PCA 결과 정규화 

◦

이미지 처리에서 유용함

•

svd_solver : svd 를 수행하는 방식을 지정

◦

‘auto’ → (default) 최적의 svd방식을 자동으로 선택

◦

‘full’ → 정확한 svd를 계산

◦

‘arpack’ → 특정 개수의 주성분만 계산할 때 사용

◦

‘randomized’ → 큰 데이터셋에 대해 근사적으로 svd를 계산해서 속도를 높인다

•

tol : ‘arpack’ 모드에서 사용하는 임곗값, 수렴 기준을 설정

◦

수렴 속도와 정확도에 영향을 줌

◦

0.0 → (default) 

•

iterated_power : ‘randomized’ 모드에서 사용하는 반복 횟수

◦

‘auto’ → (default) 

2-1. PCA 전 사전작업

•

데이터 스케일링

◦

주성분 결정시, 피처간 분산을 비교하기 때문에 필수다.

•

결측치 처리

사이킷런의 PCA 를 이용해 간단하게 구할 수 있다. 편차 또한 자동으로 처리해 계산해준다. 아래의 코드에서 singular vector 즉 주성분 행렬을 보면 위의 결과와 부호(-)가 다른 것을 확인할 수 있다. 이는 벡터의 방향만 반대일 뿐 주성분 벡터가 구성하는 축은 동일하다.

from sklearn.decomposition import PCA

# 1 <= n <= feature수
pca = PCA(n_components=n)
x_train_pc = pca.fit_transform(x_train)
x_val_prc = pca.transform(x_val)

print('singular value :', pca.singular_values_)
print('singular vector :', pca.components_.T)

# 공분산 행렬의 고유값 또한 확인할 수 있다.
print('eigen_value :', pca.explained_variance_)
# 원본 데이터의 전체 분산과 주성분 개수에 따른 분산 차이 
print('explained variance ratio :', pca.explained_variance_ratio_)
Python
복사

•

explained_variance_ratio와 적절한 차원 수 선택하기

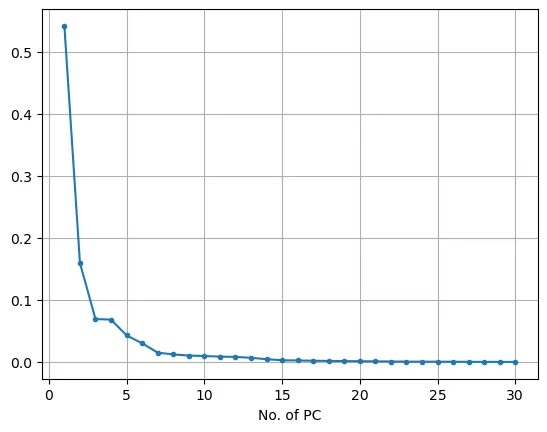
explained variance ratio는 원본데이터의 전체 분산 대비 누적 주성분의 비율 차이를 나타낸다. explained variance ratio 의 결과값을 통해 축소할 차원의 수를 결정할 수 있다. 예를 들어 누적된 분산 비율과 전체 분산의 차이가 차원이 증가함에 따라 큰 차이가 나지 않는 구간을 선택하는 것과 같다.

plt.plot(range(1,n+1), pca.explained_variance_ratio_, marker='.')
plt.xlabel('Number of PC')
plt.grid()
plt.show()
Python
복사

적정 PCA 개수는 Elbow 지점 근방에서 찾으면 좋다.

2-2. 사이킷런 PCA 실습

### 필요한 라이브러리 불러오기 ###
# 임의의 머신러닝 모델 가져오기
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import *

# 고차원 데이터를 위한 데이터 로딩
from sklearn.datasets import load_breast_cancer

# pca를 위한 데이터 스케일링
from sklearn.preprocessing import MinMaxScaler


# pca
from sklearn.decomposition import PCA
Python
복사

# 데이터 로딩
cancer = load_breast_cancer()

# x, y 설정
x = cancer.data
y = cancer.target

x = pd.DataFrame(x, columns=cancer.feature_names)
x.shape #(569, 30) -> 피처수가 많기때문에 차원 축소 필요

# 스케일링
scaler = MinMaxScaler()
x_scaled =scaler.fit_transform(x) # 변환 후 array

# 데이터프레임 변환
x = pd.DataFrame(x_scaled, columns=cancer.feature_names)

# train, validation 분할
x_train, x_val, y_train, y_val = train_test_split(x, y, test_size=0.3, random_state=0)


# 주성분 분석 : 일단 전체 피처수로 pca 진행 후, pca 수가 증가함에 따라 분산 비율 차이 시각화
n = x_train.shape[1]
pca = PCA(n_components=n)

x_train_pc = pca.fit_transform(x_train)
x_val_pc = pca.transform(x_val)

# 편하게 사용하기 위해서 데이터프레임으로 변환
columns_names = ['PC'+str(i+1) for i in range(n)] # 'PC1','PC2', ...'PC31'
x_train_pc = pd.DataFrame(x_train_pc, columns=column_names)
x_val_pc = pd.DataFrame(x_val_pc, columns = column_names)


# 주성분 누적 분산 그래프
plt.plot(range(1,n+1), pca.explained_variance_ratio_, marker='.')
plt.xlabel('Number of PC')
plt.grid()
plt.show()
Python
복사

# 주성분 개수에 따른 실제 모델 성능 시각화
result = []
for n in range(1, 31):
		cols = column_names[:n]
		x_train_pc_n = x_train_pc[cols]
		x_val_pc_n = x_val_pc[cols]
		
		# 모델링
		model = KNeighborsClassifier()
		model.fit(x_train_pc_n, y_train)
		
		pred = model.predict(x_val_pc_n)
		
		result.append(accuracy_score(y_val, pred))
		
		

plt.plot(range(1,31), result, marker='.')
plt.grid()
plt.show()
Python
복사

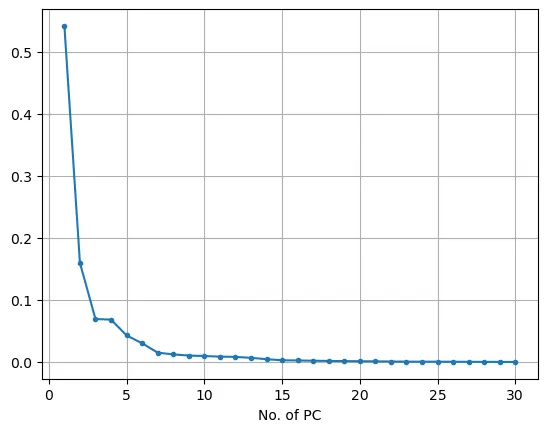
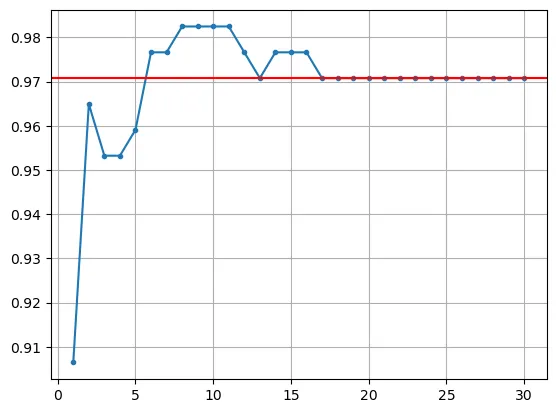
기존 30개의 변수를 모두 사용하는 것보다 주성분 6~7개를 사용했을 때 정확도가 더 높게 나오는 것을 확인할 수 있다.

n 이라는 차원수를 지정해줄 수도 있지만, 분산의 유지 비율을 통해서도 pca가 가능하다.

예를들어, MNIST 데이터셋 분산 95% 유지하도록 PCA 진행하면 다음과 같이 데이터셋의 크기가 줄어들게 된다.

from tensorflow.keras.datasets import mnist

# MNIST load
(train_x, train_y), (test_x, test_y) = mnist.load_dataset()

# reshape
train_x = train_x.reshape(-1,28*28)

pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(train_x) # pca 계산 후 투영

print('선택한 차원(픽셀) 수 :', pca.n_components_) # 154
Python
복사
PCA 적용결과 총 784 차원에서 154로 80%정도 차원이 축소된 것을 알 수 있다. 

이렇게 압축한 데이터셋을 이용해 분류 알고리즘을 학습한다면 모델 속도가 더욱 빨라질 수 있다.

또한, 압축한 데이터셋에 PCA 투영을 반대로 적용하여 다시 원 데이터의 차원으로 복원할 수 있다. 위의 경우에는 5% 만큼의 정보(분산)을 잃었기 때문에 완벽하게 복원을 할 수는 없지만, 원본 데이터와 비슷하게 복원할 수 있다. 이렇게 원본 데이터와 복원한 데이터간의 평균 제곱 거리를 재구성 오차라고 한다.

압축 후 복원하는 과정을 식으로 나타내면 다음과 같다.

X_(recovered) = X_(d-proj) V^T_d

•

X(d−proj)=XVdX_(d-proj) = XV_dX(​d−proj)=XVd​

•

Vd=orthogonalmatrix−>VdVdT=IV_d = orthogonal  matrix -> V_dV^T_d = IVd​=orthogonalmatrix−>Vd​VdT​=I

아래 코드는 위에서 압축한 X-reduced 에다가 PCA의 inverse_transform() 메소드를 이용해 784 차원으로 복원한 것이다.

X_recovered = pca.inverse_transform(X_reduced)
Python
복사

이미지 차원 축소

이미지 데이터에 대해서도 차원 축소를 진행할 수 있다.

< 필요한 패키지 및 라이브러리 > - PIL( python Imaging Library) : 이미지 처리와 조작을 위한 라이브러리 - 이미지 파일의 열기, 저장, 편집, 변환 등에 이 라이브러리를 사용함 - 여러 가지 이미지 포맷(JPEG, PNG, BMP, GIF)을 지원 - OpenCV 나 Numpy와의 호환성

다음과 같은 순서로 진행한다.

이미지의 RGB 채널을 분리

각 채널에 독립적으로 PCA를 적용해 차원을 축소

PCA로 변환된 데이터를 다시 원래의 공간으로 복원하여 채널을 결합하고, 최종 이미지를 생성한다.

위의 과정을 통해서 어떻게 차원을 축소하는지 시각적으로 확인 가능하다.

import pandas as pd 
import numpy as np
from PIL import Image # 이미지 파일을 열거나 새로 만들기 위해 불러옴
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
submission = pd.read_csv('sample_submission.csv')

# PCA를 수행할 때 ID와 타겟의 정보는 불필요하므로 제거
train = train.drop(['ID', 'Outcome'], axis = 1)
test = test.drop(['ID'], axis = 1)
display(train.head())

# 결측치 처리 및 스케일링
columns_to_replace = ['Pregnancies', 'Glucose', 'BloodPressure', 
                      'SkinThickness', 'Insulin', 'BMI']

for col in columns_to_replace:
		mean_value = train[col].replace(0, np.nan).mean() # 여기서 원본은 변경되지 않음
		train[col] = train[col].replace(0, mean_value)  # 여기서 원본이 변경됨
		test[col] = test[col].replace(0, mean_value)

scaler = StandardScaler()
scaled_train = scaler.fit_transform(train)
scaled_test = scaler.transform(test)

# svd 수행해보기(not sklearn)
# PCA는 Vt만 사용해서 주성분 추출함
# full_matrices = True : 경제적인 SVD 수행
U, S, Vt = np.linalg.svd(scaled_train, full_matrices=False)
print(f'Vt의 shape은 {Vt.shape}입니다.') # 열의 수만큼의 정방행렬

# 예시 이미지 파일을 넘파이 배열로 변환
original_image = Image.open('car.jpg') # 이미지 파일 경로 및 url
image_array = np.array(original_image)

# 원본 이미지 확인
plt.figure(figsize=(8, 4))
plt.imshow(image_array) # 2D 이미지 데이터를 시각화하는 데 사용 -> PIL.Image 객체나 Numpy 배열 형태의 이미지 데이터를 화면에 띄울 때 사용
plt.axis('off')
plt.show()
Python
복사

Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age
0	4	103	60	33	192	24.0	0.966
1	10	133	68	0	0	27.0	0.245
2	4	112	78	40	0	39.4	0.236
3	1	119	88	41	170	45.3	0.507
4	1	114	66	36	200	38.1	0.289

# RGB 채널 분리
r = image_array[:,:,0]
g = image_array[:,:,1]
b = image_array[:,:,2]

# 각 채널에 대해 PCA 수행
pca_R = PCA(n_components=0.8, svd_solver='full')
pca_G = PCA(n_components=0.8, svd_solver='full')
pca_B = PCA(n_components=0.8, svd_solver='full')

pca_R.fit(r)
pca_G.fit(g)
pca_B.fit(b)

R_transformed = pca_R.transform(r)
G_transformed = pca_G.transform(g)
B_transformed = pca_B.transform(b)

# 변환된 데이터로부터 각 채널 복원
R_restored = pca_R.inverse_transform(R_transformed)
G_restored = pca_G.inverse_transform(G_transformed)
B_restored = pca_B.inverse_transform(B_transformed)


# 복원된 채널을 결합하여 최종 이미지 생성
# np.stack 함수의 axis = -1 ==>  새로운 차원이 마지막 차원으로 추가됨
image_restored = np.stack((R_restored, G_restored, B_restored), axis=-1)
Python
복사

# 원본 이미지와 복원된 이미지 시각화 및 저장
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
ax[0].imshow(image_array)
ax[0].set_title('Original Image')
ax[0].axis('off')

ax[1].imshow(image_restored.astype('uint8'))
ax[1].set_title('Restored Image')
ax[1].axis('off')

plt.show()
Python
복사
‘uint8’ 데이터 타입은 8비트 양의 정수로, 값의 범위는 0 ~ 255
주로 이미지 데이터를 표현할 때 사용 → 이미지의 픽셀 값이 보통 0에서 255 사이의 값을 가지기 때문

이미지에 PCA를 적용한 결과, 전체 성분의 80%만으로도 이미지의 윤곽이 상당 부분 유지되는 것을 확인할 수 있다. PCA가 데이터의 특성을 효과적으로 추출하고 축소할 수 있음을 보여준다.

PCA 의 장단점

[ 장점 ]

•

데이터의 중요한 특성을 유지하며 차원을 줄이고, 복잡성을 감소시킨다.

•

불필요한 변동성을 제거해서 핵심 특성을 더 명확하게 드러낸다.

•

저차원으로 변환해주니 시각화와 해석이 용이하다.

[ 단점 ]

•

결측치를 해결하고, 스케일링을 진행해야 주성분을 제대로 계산할 수 있다.

•

pca는 분산의 크기만 고려한 선형축소방식이다.

→ 따라서, 저차원에서 특징을 잘 담아내지 못하는 경우가 종종 발생한다.

→ 이를 보완한 방법이 t-SNE다.

•

주성분은 원본 변수들의 선형 결합으로 구성되므로 이들이 무엇을 의미하는지 해석하기 어려울 수 있다.

•

모든 변수가 동일한 중요도를 가지고 있다고 가정하므로, 어떤 변수가 더 중요한지 구별하기 어렵습니다.

2. LDA - 선형 판별 분석(지도 학습)

고차원 데이터를 저차원으로 축소하는 데 사용되는 기법

- 분류 문제에서 데이터의 클래스를 가장 잘 구분할 수 있는 축을 찾는 데 초점을 맞춤

- 클래스 간 분산은 최대화하고, 클래스 내 분산은 최소화 하는 방식으로 작동

즉, 분류 문제에서 클래스 구분을 더 쉽게 만들어줄 수 있는 분석 방법 중 하나다(지도 학습)

LDA 장점

•

 LDA는 분류 작업에서 PCA보다 높은 성능을 발휘한다

•

데이터의 클래스별 평균 차이가 클 때 탁월한 성능

•

분산 구조가 일정한 가정이 위반되더라도 비교적 잘 작동

LDA 단점

•

클래스 불균형, 비정규 분포, 다중 공선성과 같은 데이터의 특정한 특성에 의해서 LDA의 성능이 영향을 받을 수 있음

•

클래스 수에 따라 생성할 수 있는 성분의 수가 제한됨

•

데이터가 정규분포를 따른다고 가정하므로, 이 가정에서 벗어나면 성능이 저하될 수 있음

sklearn 에서 사용하기

•

LDA 파라미터

◦

solver : 모델을 학습시킬 때 사용되는 알고리즘

▪

‘svd’(특이값 분해) , ‘lsqr’, ‘eigen’(고윳값 분해)

◦

shrinkage : ‘lsqr’ , ‘eigen’ 의 경우에만 사용

▪

공분산 추정에 대한 정규화 적용

▪

샘플 수(n)보다 특성(m)이 많은 경우에 유용

▪

default → None

◦

priors : 클래스별 사전 확률. 기본적으로 클래스 빈도에 따라 자동으로 계산.  but 직접 지정할 수도 있음

◦

n_components : 축소할 차원의 수

▪

default → None (클래스의 수 - 1 ,  피처의 수 중, 작은 값으로 설정)

◦

tol : ‘svd’ solver에서는 사용되지 않음. 수치적 안정성을 위한 공분산 행렬의 절단 기준값

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

lda = LDA()

lda.fit(scaled_train, y_train) # 지도 학습이기 때문에 y_train 필요
lda_transformed_train = lda.transform(scaled_train)

lda_columns = [f'lda{i + 1}' for i in range(lda_transformed_train.shape[1])]

lda_df = pd.DataFrame(lda_transformed_train, columns=lda_columns)
Python
복사

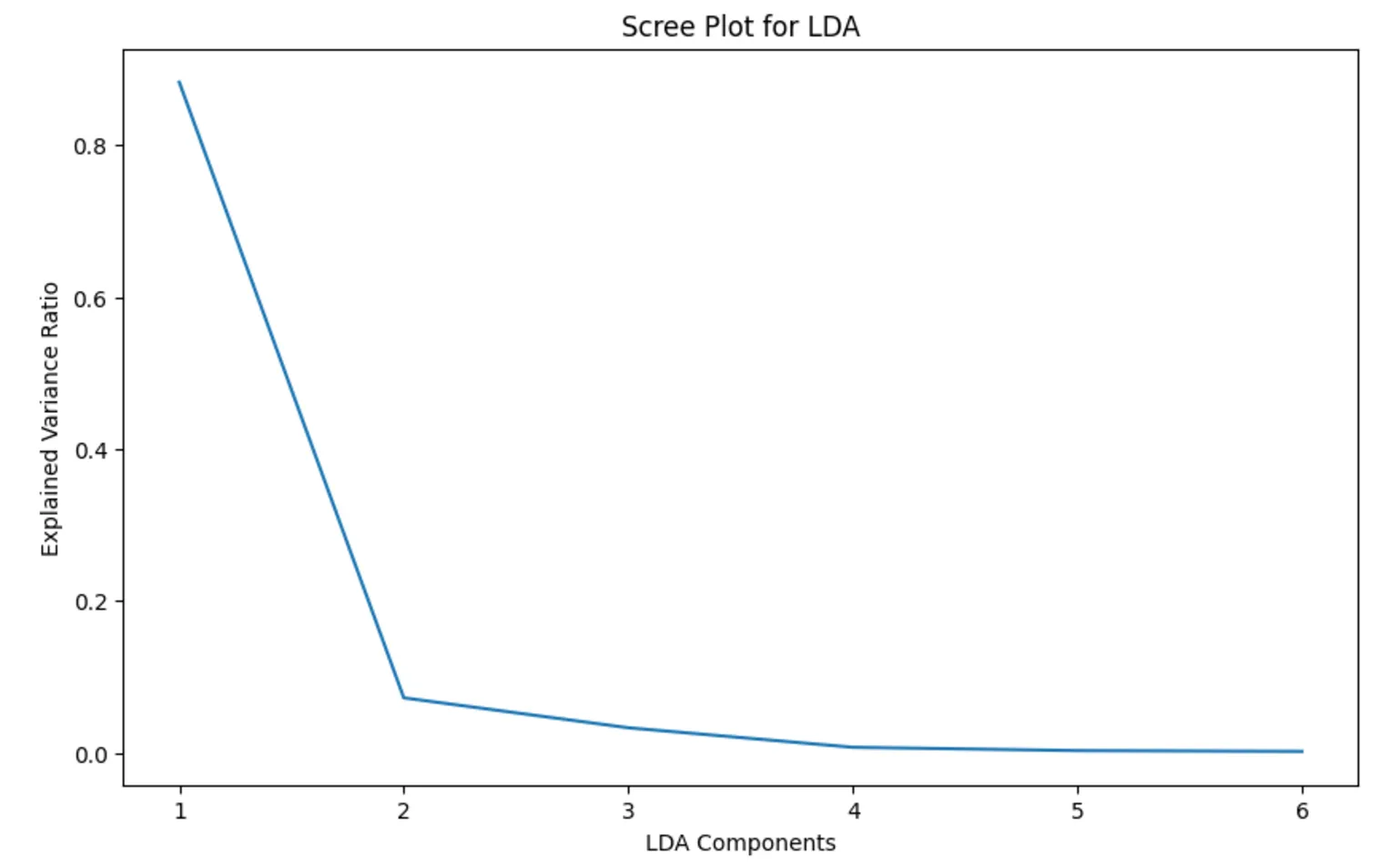
Screeplot - 최적의 차원 수 찾아내기

얼마가 최적의 차원 수일까?

일반적으로 차원 축소된 차원의 설명된 분산 비율 목표를 70 ~ 90% 사이로 설정한다고 한다.

이를 만족하는 지점을 Elbow라고 부른다.

차원 축소를 수행한 뒤의 특성이 설명하는 분산의 비율을 시각적으로 확인할 수 있다.

•

explained_variance_ratio_ 메소드 사용

plt.figure(figsize=(10,6))
plt.plot(range(1, lda_transformed_train.shape[1] + 1), lda.explained_variance_ratio_)
plt.xlabel('LDA Components')
plt.ylabel('Explained Variance Ratio')
plt.title('Scree plot for LDA')
plt.show()
Python
복사

두 번째 주성분에서 분산의 비율이 급격하게 감소한다. 이 지점이 Elbow → 최적의 차원을 2로 설정한다.

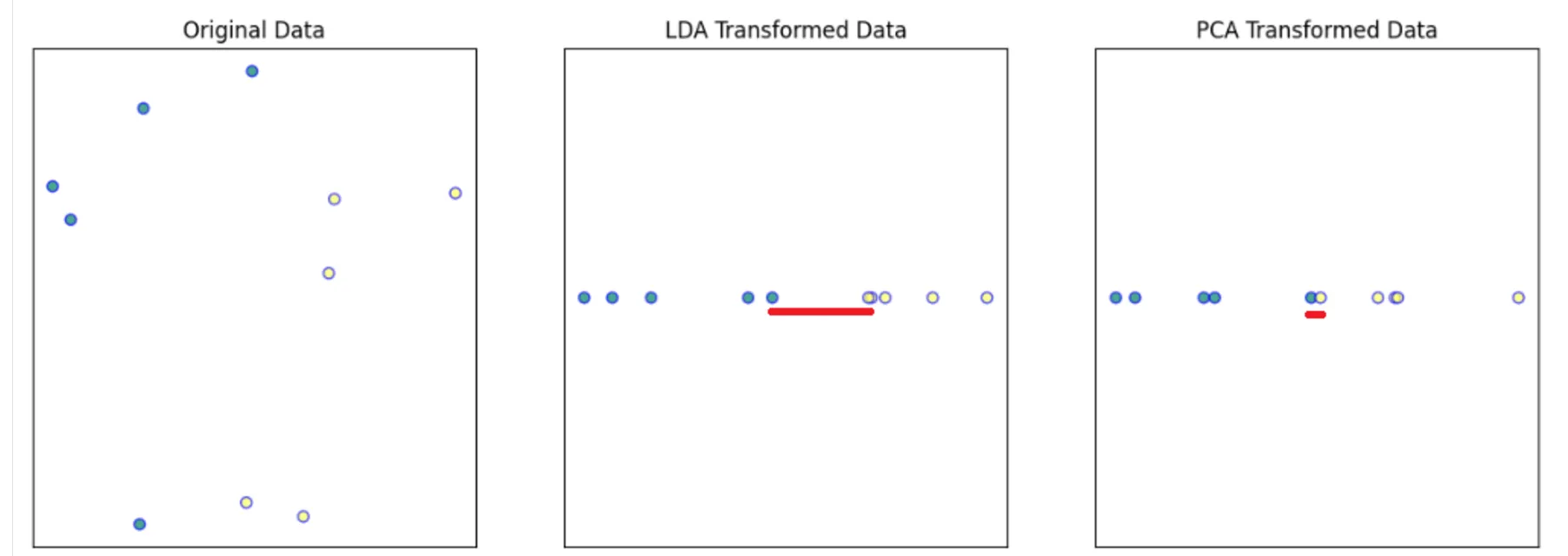
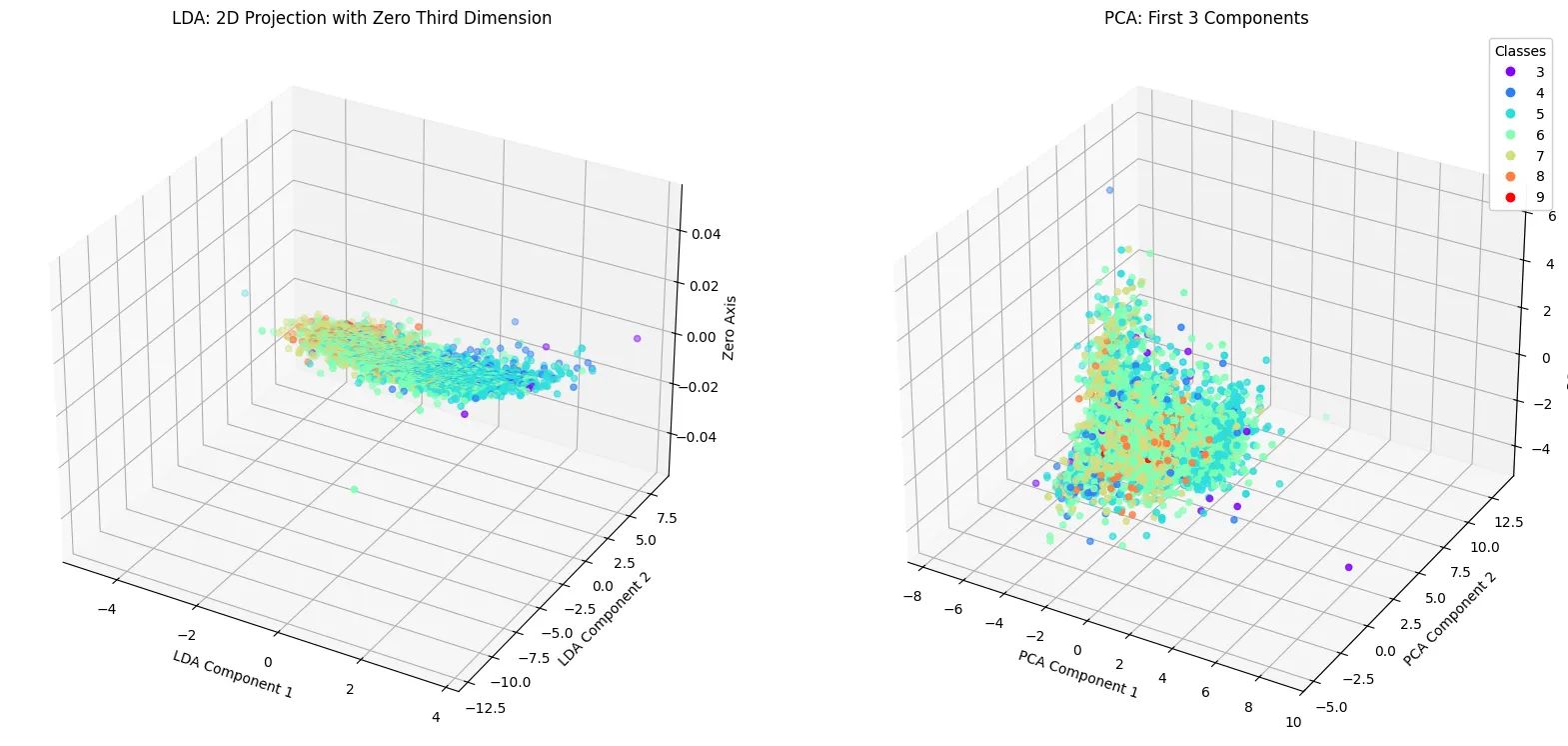
LDA와 PCA 변환 데이터의 3D 시각화

차원이 축소된 데이터를 3차원 공간에서 시각화하는 방법을 알아보자.

LDA와 PCA를 통해 차원이 축소된 데이터를 3D로 시각화하는 것은 데이터의 중요한 특성을 직관적으로 이해하고 해석하는 데 도움을 줍니다.

2D 의 경우, 3D 시각화를 위해 세 번째 축을 추가해보도록 한다.

from mpl_toolkits.mplot3d import Axes3D #  실제로 Axes3D가 사용되지는 않지만 Matplotlib의 3D plotting 기능을 활성화할 수 있음

fig = plt.figure(figsize=(20,10))

# LDA 3D 시각화(가상의 3번째 축 추가)
ax = fig.add_subplot(1, 2, 1, projection='3d')
scatter = ax.scatter(xs = lda_transformed_train[:,0], ys = lda_trasformed_train[:,1], zs = np.zeros_like(lda_transformed_train[:,0]),
											c = y_train, cmap = plt.cm.rainbow)
ax.set_title('LDA : 2D Projection with Zero Third Dimension')
ax.set_xlabel('LDA Component 1')
ax.set_ylabel('LDA Component 2')
ax.set_zlabel('Zero Axis')


# PCA 3D 시각화(처음 세 주성분 사용)
ax = fig.add_subplot(1, 2, 2, projection='3d')
scatter = ax.scatter(xs = pca_transformed_train[:,0], ys = pca_transformed_train[:,1], zs = pca_transformed_train[:,2],
											c = y_train, camp = plt.cm.rainbow)
ax.set_title('PCA: First 3 Components')
ax.set_xlabel('PCA Component 1')
ax.set_ylabel('PCA Component 2')
ax.set_zlabel('PCA Component 3')

legend = ax.legend(*scatter.legend_elements(), title='Classes')
ax.add_artist(legend)

plt.show()
Python
복사

3. t - SNE

•

원본의 특성을 최대한 살리면서 축소하는 방법으로 고안된 모델이다.

◦

즉, 원본에서 가까운 거리의 점들은 축소한 뒤에도 가깝게 만들자는 것이 이 모델의 목적이다.

◦

비선형 방식이다.

•

주로 데이터 시각화를 위해 사용된다.

•

학습하는데 오래걸린다는 단점이 있다.

•

보통 고차원 → 2 , 3 차원으로 축소한다.

3-1. t - SNE 활용하기

•

사전작업

◦

스케일링

▪

유사도 맵을 만들 때 유클리드 거리 계산을 활용하기 때문

•

사이킷런

from sklearn.manifold import TSNE

# 2차원으로 축소
tsne = TSNE(n_components=2)
x_tsne = tsne.fit_transform(x)
Python
복사

3-2 절차

원본 데이터에서 유사도 맵  만들기

하나의 데이터 포인트에서 다른 데이터들과 유클리드 거리 계산

거리를 유사도로 변환 : t-분포로 유사도 계산

ii.

각 유사도를 전체 유사도 합으로 나눠서 스케일링

iii.

유사도 맵 만들기

다른 데이터 포인트에서도 동일한 작업 수행

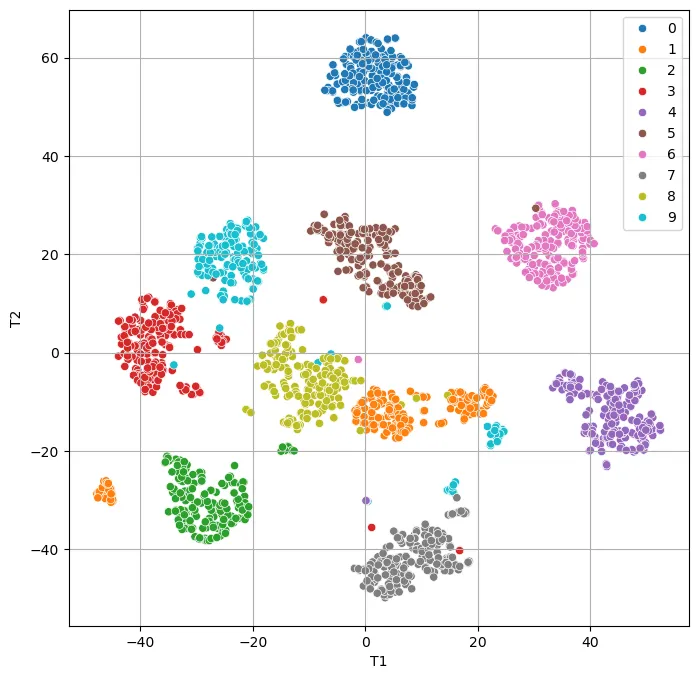
3-3. t - SNE 실습

from sklearn.manifold import TSNE

digits = load_digits()
x = digits.data
y = digits.target

y = y.astype('categorical')
x.shape # (1797,64)

# 스케일링 - digits 데이터의 특성상 수동으로 스케일링 : 최댓값으로 나누면 MinMax 스케일링이 됨
x = x / np.max(x)


# 2차원으로 축소 및 시각화(2차원이라 가능)
tsne = TSNE(n_components=2, random_state=0)
x_tsne = tsne.fit_transform(x)

# 데이터프레임으로 변환
x_tsne = pd.DataFrame(x_tsne, columns=['T1' ,'T2'])

# 시각화
plt.figure(figsize=(8,8))
sns.scatterplot(x='T1', y='T2', data=x_tsne, hue=y)
plt.grid()
plt.show()
Python
복사

4. incremental PCA (IPCA)

PCA의 단점은 SVD를 수행하기 위해서는 전체 학습 데이터셋을 메모리에 올려야 한다는 것이다. 이런 단점을 보완하기 위해 incremental pca 알고리즘이 개발되었다.

IPCA는 학습 데이터셋을 미니배치로 나눈 뒤 IPCA 알고리즘에 하나의 미니배치를 입력으로 넣어준다. IPCA는 학습 데이터셋이 클때 유용하다.

사이킷런에서는 IncrementalPCA를 통해 incremental PCA를 사용할 수 있다. 아래의 코드는 다시 MNIST 데이터를 100개의 미니배치로 나눠 PCA를 수행한 것이다.

from sklearn.decomposition import IncrementalPCA

n_batches=100
inc_pca = IncrementalPCA(n_components=154)
for batch_x in np.array_split(train_x, n_batches):
	print(".", end="")
	inc_pca.partial_fit(batch_x)

X_reduced = inc_pca.transform(train_x)

X_recovered_inc_pca = inc_pca.inverse_transform(X_reduced)
Python
복사

5. kernal PCA

서포트벡터머신에서 커널을 이용해 데이터를 저차원에서 고차원으로 매핑시켜 데이터셋에 SVM를 적용시키는 kernal SVM이 있다.

이 기법을 PCA에 적용해 비선형 투영으로 차원을 축소할 수 있는데, 이것을 Kernal PCA(KPCA)라고 한다.

사이킷런의 KernalPCA 를 통해 적용할 수 있다.

from sklearn.datasets import make_swiss_roll

X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)

from sklearn.decomposition import KernalPCA

rbf_pca = KernalPCA(n_components=2, kernal='rbf', gamma=0.04)
X_reduced = rbf_pca.fit_transform(X)

Python
복사