레이블 값의 분포가 불균형한 데이터의 예시다. 이상현상을 감지하는 클래스는 전체 데이터에서 차지하는 비중이 매우 적을 수밖에 없다.
언더 샘플링과 오버 샘플링의 이해
레이블 데이터의 분포가 비대칭일 경우, 정상 클래스는 상대적으로 데이터수가 많기 때문에 학습을 많이 하고 적은 데이터수를 가지고 있는 이상 클래스는 학습량이 적을 것이다. 따라서 학습 자체가 불균형하게 학습되는 것이다.
이렇게 지도학습에서의 레이블 분포가 불균형적인 상황에서의 대안은 두가지로 나뉘는데,
오버 샘플링과 언더 샘플링이다.
일반적으로 오버 샘플링이 예측 성능상 더 유리한 경우가 많기 때문에 주로 사용된다.
•
오버 샘플링 : 적은 레이블을 가진 데이터 세트를 많은 레이블을 가진 데이터 세트 수준으로 증식하는 것
→ 원본 데이터의 값들을 아주 약간 변형하여 증식. 대표적으로 SMOTE 방법
•
언더 샘플링 : 많은 레이블을 가진 데이터 세트를 적은 레이블을 가진 데이터 세트 수준으로 감소시키는 것
→ 단점 : 정상 레이블의 경우 오히려 제대로 된 학습을 수행할 수 없음.
SMOTE를 구현한 대표적인 파이썬 패치지는 imbalanced-learn 이다.
일단, 아나콘다를 이용해 imbalanced-learn 패키지를 설치한다.
명령 프롬프트에 conda install -c conda-forge imbalanced-learn 입력
데이터 일차 가공 및 모델 학습/예측/평가
데이터를 DataFrame으로 로딩하겠다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
card_df = pd.read_csv('creditcard.csv')
card_df.head(3)
'''
3 rows × 31 columns
'''
Python
복사
일단, Time 피처는 크게 의미가 없어보이므로 삭제한다. Amount는 거래 금액을 의미한다. Class는 정상 거래면 0, 사기 거래면 1로 구분한다.
card_df.info()
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Time 284807 non-null float64
1 V1 284807 non-null float64
2 V2 284807 non-null float64
3 V3 284807 non-null float64
4 V4 284807 non-null float64
5 V5 284807 non-null float64
6 V6 284807 non-null float64
7 V7 284807 non-null float64
8 V8 284807 non-null float64
9 V9 284807 non-null float64
10 V10 284807 non-null float64
11 V11 284807 non-null float64
12 V12 284807 non-null float64
13 V13 284807 non-null float64
14 V14 284807 non-null float64
15 V15 284807 non-null float64
16 V16 284807 non-null float64
17 V17 284807 non-null float64
18 V18 284807 non-null float64
19 V19 284807 non-null float64
20 V20 284807 non-null float64
21 V21 284807 non-null float64
22 V22 284807 non-null float64
23 V23 284807 non-null float64
24 V24 284807 non-null float64
25 V25 284807 non-null float64
26 V26 284807 non-null float64
27 V27 284807 non-null float64
28 V28 284807 non-null float64
29 Amount 284807 non-null float64
30 Class 284807 non-null int64
dtypes: float64(30), int64(1)
memory usage: 67.4 MB
'''
Python
복사
일단, 결측치는 없고, 모두 수치형데이터이며, 총 31개의 속성이 존재하고 284807개의 데이터개수가 있다.
이번 실습에서는 보다 데이터 사전 가공을 더 열심히 할 것이기 때문에 본 데이터를 가공하여 변환하는 함수 get_preprocessed_df() 함수와 가공 후 학습/테스트 데이터 세트를 반환하는 get_train_test_df() 함수를 생성하자.
1.
get_preprocessed_df() 함수
일단, Time속성을 삭제하고
from sklearn.model_selection import train_test_split
# 인자로 입력받은 DataFrame을 복사한 뒤 Time칼럼만 삭제하고 복사된 DataFrame 반환
def get_preprocessed_df(df=None):
df_copy = df.copy()
df_copy.drop('Time',axis=1,inplace=True)
return df_copy
Python
복사
2.
get_train_test_df() 함수
get_preprocessed_df()함수를 호출하고 학습데이터와 테스트 데이터 세트를 반환한다. 내부에서 train_test_split() 함수 호출한다. 참고로, 불균형한 레이블값을 가지고 있으므로 나눌때 stratified 방식으로 추출해 레이블 값 분포도를 동일하게 만들어야 한다.
# 사전 데이터 가공 후 학습과 테스트 데이터 세트를 반환하는 함수.
def get_train_test_df(df=None):
# 사전 가공된 데이터 프레임 호출
df_copy = get_preprocessed_df(df)
# 일단, 레이블 데이터세트와 피처 데이터 세트 분할
X_features = df_copy.iloc[:,:-1]
y_target = df_copy.iloc[:,-1]
# train_test_split()으로 학습과 테스트 데이터 분할. stratify=y_target 사용
X_train,X_test,y_train,y_test = train_test_split(X_features,y_target,test_size=0.3,random_state=0,stratify=y_target)
# 학습과 테스트 데이터 세트 반환
return X_train,X_test,y_train,y_test
Python
복사
X_train,X_test,y_train,y_test = get_train_test_df(card_df)
Python
복사
제대로 레이블 분포가 분리되어있는지 확인해보자.
print('학습 데이터 레이블 값 비율')
print(y_train.value_counts()/y_train.shape[0]*100) # 백분율로 환산
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/y_test.shape[0]*100)
'''
학습 데이터 레이블 값 비율
0 99.827451
1 0.172549
Name: Class, dtype: float64
테스트 데이터 레이블 값 비율
0 99.826785
1 0.173215
Name: Class, dtype: float64
'''
Python
복사
원본 레이블 분포의 형태와 비슷하게 잘 분리가 되어있는 것을 확인했다.
이제, 모델을 만들어보자. 우리는 로지스틱 회귀와 LightGBM 기반의 모델에 대해서 먼저 비교하고 알아볼 것이다.
a.
로지스틱 회귀
예측 성능 평가는 앞서 생성한 get_clf_eval() 함수를 재사용할 것이다.
from sklearn.linear_model import LogisticRegression
lr_clf = LogisticRegression()
lr_clf.fit(X_train,y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:,1]
# 3장에서 사용한 get_clf_eval() 함수를 이용해 평가
get_clf_eval(y_test,lr_pred,lr_pred_proba)
'''
오차 행렬
[[85282 13]
[ 60 88]]
정확도:0.9991, 정밀도:0.8713, 재현율:0.5946, f1 스코어:0.7068, AUC : 0.9572
'''
Python
복사
이제, 다양한 모델을 통해서 예측 평가를 할 것이기 때문에 아예 함수를 만들어보자.
get_model_train_eval() 함수는 인자로 estimator객체와 학습/테스트 데이터 세트를 입력받아서 학습/예측/평가를 모두 수행할 것이다.
def get_model_train_eval(model,ftr_train=None,ftr_test=None,tgt_train=None,tgt_test=None):
model.fit(ftr_train,tgt_train)
pred = model.predict(ftr_test)
pred_proba = model.predict_proba(ftr_test)[:,1]
get_clf_eval(tgt_test,pred,pred_proba)
Python
복사
b.
LightGBM
레이블 분포도가 극도로 불균형할 경우 LGBMClassifier객체 생성 시 boost_from_average=False를 파라미터로 설정해줘야 한다.
•
boost_from_average=True가 default값이다. 레이블 값이 극도로 불균형한 분포를 이룰 경우 재현률 및 roc-auc 성능이 매우 저하된다.
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000,num_leaves=64,n_jobs=-1,boost_from_average=False)
get_model_train_eval(lgbm_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
'''
오차 행렬
[[85290 5]
[ 36 112]]
정확도:0.9995, 정밀도:0.9573, 재현율:0.7568, f1 스코어:0.8453, AUC : 0.9790
'''
Python
복사
로지스틱 회귀의 결과보다는 높은 수치가 나왔다.
데이터 분포도 변환 후 모델 학습/예측/평가
이번에는 아예 데이터 분포를 재가공한 뒤에 모델에 적합시켜 본다.
먼저, 피처들의 분포들을 살펴본다.
일단, 선형 모델은 피처들의 분포가 정규 분포 형태를 유지하는 것을 중요하게 생각한다.
Amount 속성은 레이블값의 결정에 영향을 미치는 중요한 피처라고 예상된다. 이 피처의 분포부터 살펴보자.
import seaborn as sns
plt.figure(figsize=(8,4))
plt.xticks(range(0,30000,1000),rotation=60)
sns.distplot(card_df['Amount'])
Python
복사
여기서 xticks의 rotation은 x축 레이블텍스트의 시계반대방향 회전각도를 의미한다. 레이블이 길 경우 곂치지 않게하기 위해서 사용.
참고로 seaborn의 distplot은 히스토그램을 그리는 시각화 그래프다. 수치 변수가 하나일 경우에 쓰인다. 여러 변수의 분포를 비교할때는 박스플롯 또는 바이올린 플롯을 수행하는 것이 더 좋다.
sns.distplot(df[’변수’], bins=None, hist=True, kde=True, rug=True, color=None, vertical=False,...)
bins는 빈의 갯수를 조정하는 방식이다. color는 막대그래프의 색깔을 지정해주는 방식이다. vertical=True로 지정하면 그래프를 세로축 중심으로 그릴 수 있다.
어쨌든, Amount특성의 분포를 살펴보니 거의 모든 데이터가 1000불 이하였다. 드물지만 큰 값들이 종종 나와서 꼬리가 긴 분포를 띄고 있다.
이제, Amount를 표준정규분포 형태로 변환을 해보자. (StandardScaler 클래스를 사용)
from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardScaler를 이용해 정규 분포 형태로 Amount 피처값 변환하는 로직으로 수정.
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1,1))
# 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 칼럼으로 입력
df_copy.insert(0,'Amount_Scaled',amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy
Python
복사
# Amount를 정규 분포 형태로 변환 후 로지스틱 회귀 및 LightGBM 수행
X_train,X_test,y_train,y_test = get_train_test_df(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
lgbm_clf = LGBMClassifier(n_estimators=1000,num_leaves=64,n_jobs=-1)
get_model_train_eval(lgbm_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
'''
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85281 14]
[ 58 90]]
정확도:0.9992, 정밀도:0.8654, 재현율:0.6081, f1 스코어:0.7143, AUC : 0.9702
### LightGBM 예측 성능 ###
오차 행렬
[[85146 149]
[ 81 67]]
정확도:0.9973, 정밀도:0.3102, 재현율:0.4527, f1 스코어:0.3681, AUC : 0.7253
'''
Python
복사
결과는 두 모델 모두 이전과 비교해 성능이 오히려 떨어졌다.
이번에는 표준화가 아니라 로그 변환을 수행해보자. 로그변환은 데이터 분포도가 심하게 왜곡되어 있을 경우 적용하는 중요 기법 중 하나다.
넘파이의 log1p()함수를 이용해 간단히 변환이 가능하다.
앞서 만든 get_preprocessed_df() 함수를 변경해보자.
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount'])
# 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 칼럼으로 입력
df_copy.insert(0,'Amount_Scaled',amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy
Python
복사
X_train,X_test,y_train,y_test = get_train_test_df(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
'''
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85283 12]
[ 59 89]]
정확도:0.9992, 정밀도:0.8812, 재현율:0.6014, f1 스코어:0.7149, AUC : 0.9727
### LightGBM 예측 성능 ###
오차 행렬
[[85238 57]
[ 77 71]]
정확도:0.9984, 정밀도:0.5547, 재현율:0.4797, f1 스코어:0.5145, AUC : 0.7395
'''
Python
복사
마찬가지로 큰 차이가 없다.
이상치 데이터 제거 후 모델 학습/예측/평가
이상치를 찾아내는 방법과 제거한 뒤 모델 평가를 해보겠다.
먼저, IQR방식은 사분위값의 편차를 이용하는 기법으로 박스 플롯방식으로 시각화할 수 있다. IQR은 1/4 지점과 3/4지점 사이의 범위다.
이상치는 IQR*1.5를 더하고 빼서 생성된 범위보다 크거나 작으면 이상치로 간주한다.
물론, 꼭 1.5가 아니어도 된다.
이제, 위의 방식을 사용해서 이상치를 제거해보자. 특성치들이 많을 경우에는 레이블과 가장 상관성이 높은 특성의 이상치를 제거하는 것이 좋다.
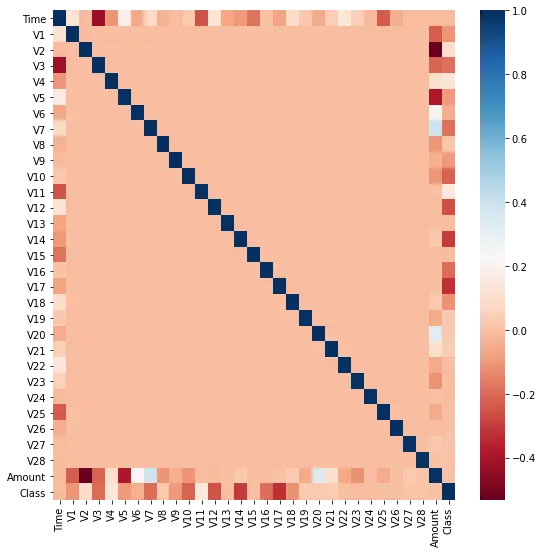
그럴러면, 레이블과의 상관정도를 아는 것이 필요하기 때문에 corr()을 사용해서 피처별 상관도를 구한 다음 seaborn의 heatmap으로 시각화해보자.
import seaborn as sns
plt.figure(figsize=(9,9))
corr = card_df.corr()
sns.heatmap(corr,cmap='RdBu')
Python
복사
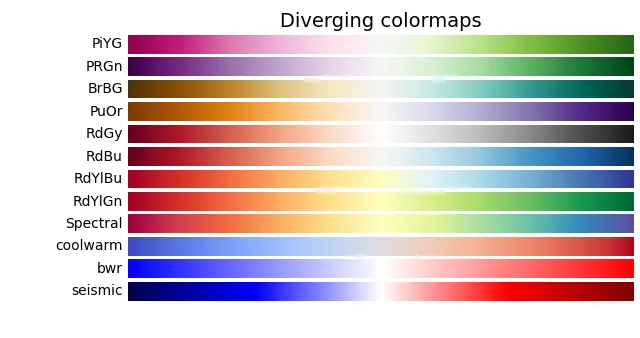
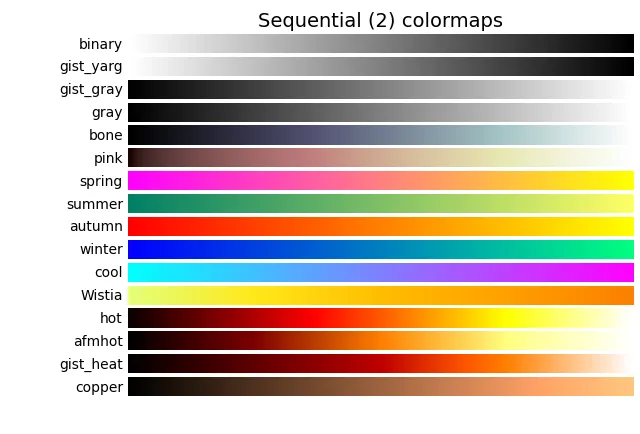
참고로 cmap 은 컬러맵을 의미하는데 다음을 참고해보자.
결론적으로 Class피처와 상관관계가 높아보이는 특성들은 V14 와 V17이다.
일단, V14에 대해서만 이상치가 있으면 제거하겠다.
이상치를 구하는 함수를 직접 만들어보겠다. get_outlier()함수이고 인자로는 DataFrame, 칼럼을 받겠다.
percentile()을 사용해서 Q1과 Q3를 구하고 IQR을 구해 범위를 구하고 그 범위보다 크거나 작으면 이상치로 설정하고 이상치인 데이터프레임의 index를 반환한다.
import numpy as np
def get_outlier(df=None, column=None, weight=1.5):
# fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함.
fraud = df[df['Class']==1][column]
quantile_25 = np.percentile(fraud.values,25)
quantile_75 = np.percentile(fraud.values,75)
# IQR을 구하고, IQR에 1.5를 곱해 최댓값과 최솟값 지점 구함.
iqr = quantile_75-quantile_25
iqr_weight = iqr*weight
lowest_val = quantile_25 - iqr_weight
highest_val = quantile_75 + iqr_weight
# 최댓값보다 크거나 최솟값보다 작은 값을 이상치 데이터로 설정하고 데이터프레임 인덱스 반환.
outlier_index = fraud[(fraud < lowest_val) | (fraud > highest_val)].index
return outlier_index
Python
복사
함수를 만들었으니, V14컬럼에서 이상치 데이터를 찾아보겠다.
outlier_index = get_outlier(df=card_df, column='V14')
print('이상치 데이터 인덱스:', outlier_index)
'''
이상치 데이터 인덱스: Int64Index([8296, 8615, 9035, 9252], dtype='int64')
'''
Python
복사
이상치로 판단된 데이터의 개수는 4개이며 각각의 인덱스는 위와 같다.
이번에는 get_outlier함수를 사용해서 이상치를 추출하고 아예 삭제까지 하는 로직을 get_preprocessed_df() 함수에 추가해보겠다.
# get_preprocessed_df()를 로그 변환 후 V14피처의 이상치 데이터를 삭제하는 로직으로 변경.
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0,'Amount_Scaled',amount_n)
df_copy.drop(['Time','Amount'],axis=1,inplace=True)
# 이상치 데이터 삭제하는 로직 추가
outlier_index = get_outlier(df=df_copy, column='V14')
df_copy.drop(outlier_index,axis=0,inplace=True)
return df_copy
X_train,X_test,y_train,y_test = get_train_test_df(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf,ftr_train=X_train,ftr_test=X_test,tgt_train=y_train,tgt_test=y_test)
'''
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85281 14]
[ 48 98]]
정확도:0.9993, 정밀도:0.8750, 재현율:0.6712, f1 스코어:0.7597, AUC : 0.9743
### LightGBM 예측 성능 ###
오차 행렬
[[85268 27]
[ 36 110]]
정확도:0.9993, 정밀도:0.8029, 재현율:0.7534, f1 스코어:0.7774, AUC : 0.9218
'''
Python
복사
이상치를 제거하고 로그 변환 하고 나니 예측 성능의 결과가 훨씬 좋아졌다.
SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가
이제 드디어 하고 싶었던 SMOTE 기법을 적용한 오버 샘플링을 적용해보고 다시 로지스틱 회귀와 LightGBM 모델의 예측 성능을 평가해보자.
앞서 설치한 imbalanced-learn 패키지의 SMOTE 클래스를 이용해서 간단하게 구현 가능하다.
이때, 주의할 점은 오버 샘플링은 반드시 학습 데이터에만 적용해야 한다.
이제, SMOTE 객체의 fit_sample() 메서드를 이용해 원 데이터를 증식한 뒤 데이터를 증식 전과 비교해보자.
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
X_train_over,y_train_over = smote.fit_sample(X_train,y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트:', X_train.shape,y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트:', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포:\n', pd.Series(y_train_over).value_counts())
'''
SMOTE 적용 전 학습용 피처/레이블 데이터 세트: (199362, 29) (199362,)
SMOTE 적용 후 학습용 피처/레이블 데이터 세트: (398040, 29) (398040,)
SMOTE 적용 후 레이블 값 분포:
0 199020
1 199020
Name: Class, dtype: int64
'''
Python
복사
데이터가 증식되었고 레이블 분포도 고르게 증가한 것을 확인했다.
이제, 로지스틱 회귀를 가지고 학습시켜보겠다.
lr_clf = LogisticRegression()
# ftr_train과 tgt_train 인자값이 SMOTE로 증식된 X_train_over,y_train_over로 변경.
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)
'''
오차 행렬
[[82937 2358]
[ 11 135]]
정확도:0.9723, 정밀도:0.0542, 재현율:0.9247, f1 스코어:0.1023, AUC : 0.9737
'''
Python
복사
오버 샘플링을 한 결과 로지스틱 모델에서는 재현율이 아주 높아졌으나 반대로 정밀도가 5.4%로 급격하게 저하되었다.
이 문제는 1의 학습이 실제보다 지나치게 학습되어 오히려 0의 예측이 저조해진것이다.
문제를 좀더 시각화해서 확인해보기 위해 분류 결정 임곗값에 따른 정밀도와 재현율 곡선을 그래프로 그려보겠다. 이때 사용할 함수는 앞서 만든 precision_recall_curve_plot() 이다.
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve
%matplotlib inline
def precision_recall_curve_plot(y_test,pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출
precisions, recalls, thresholds = precision_recall_curve(y_test,pred_proba_c1)
# x축을 threshold값으로, y축은 정밀도, 재현율 값으로 각각 plot수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary=thresholds.shape[0]
plt.plot(thresholds,precisions[0:threshold_boundary],linestyle='--',label='precision')
plt.plot(thresholds,recalls[0:threshold_boundary],label='recall')
# threshold 값 x 축의 scale을 0.1단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start,end,0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value');plt.ylabel('Precision and Recall value')
plt.legend();plt.grid()
plt.show()
Python
복사
precision_recall_curve_plot(y_test,lr_clf.predict_proba(X_test)[:,1])
Python
복사
임곗값의 민감도가 너무 심해 올바른 재현율/정밀도 성능을 얻을 수 없다는 결론이 나왔다.
이번에는, LightGBM을 가지고 한번 학습/예측/평가를 진행해본다.
lgbm_clf = LGBMClassifier(n_estimators=1000,num_leaves=64,n_jobs=-1,boost_from_average=False)
get_model_train_eval(lgbm_clf,ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)
'''
오차 행렬
[[85283 12]
[ 22 124]]
정확도:0.9996, 정밀도:0.9118, 재현율:0.8493, f1 스코어:0.8794, AUC : 0.9814
'''
Python
복사
정밀도와 재현율 측면 모두 증가했다.
하지만, 일반적으로 SMOTE를 적용하면 재현율은 높아지나 정밀도는 낮아진다.