데이터 세트는
위에서 다운로드 받는다. 위의 데이터파일에서 diabetes.csv 파일을 적당한 위치에 다운로드 받는다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, roc_auc_score
from sklearn.metrics import f1_score, confusion_matrix, precision_recall_curve, roc_curve
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
diabetes_data = pd.read_csv('diabetes.csv')
Python
복사
diabetes_data.info()
'''
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null int64
1 Glucose 768 non-null int64
2 BloodPressure 768 non-null int64
3 SkinThickness 768 non-null int64
4 Insulin 768 non-null int64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null int64
8 Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB
'''
Python
복사
일단, 데이터를 확인해보면 총 8개의 피처로 구성되어 있고 결과값은 이진분류형태로 되어있고 0 또는 1의 값을 가진다. 결측치는 없다.
print(diabetes_data['Outcome'].value_counts())
'''
0 500
1 268
Name: Outcome, dtype: int64
'''
Python
복사
일단, y 값의 종류와 그 분포를 확인해보면 Negative가 상대적으로 많은 것을 확인할 수 있다.
모든 피처들이 숫자형으로 되어있고 변수들이 나타내는 것을 보면 별도로 인코딩할 필요는 없어 보인다.
이제, 예측을 위한 과정을 만들어보겠다. 일단, y와 x 데이터 세트를 나눈 뒤, 테스트데이터와 학습데이터로 나눈다.
# x, y 데이터 나누기
X = diabetes_data.iloc[:,:-1]
y = diabetes_data.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=156,stratify=y)
# 로지스틱 회귀로 학습, 예측 및 평가 수행
lr_clf = LogisticRegression()
lr_clf.fit(X_train,y_train)
pred = lr_clf.predict(X_test)
pred_proba = lr_clf.predict_proba(X_test)[:,1]
get_clf_eval(y_test,pred,pred_proba)
'''
오차 행렬
[[88 12]
[23 31]]
정확도:0.7727, 정밀도:0.7209, 재현율:0.5741, f1 스코어:0.6392, AUC : 0.7919
'''
Python
복사
전체 데이터의 65%가 Negative(0)라서 정확도보다는 재현율 성능에 좀 더 초점을 맞춰보겠다.
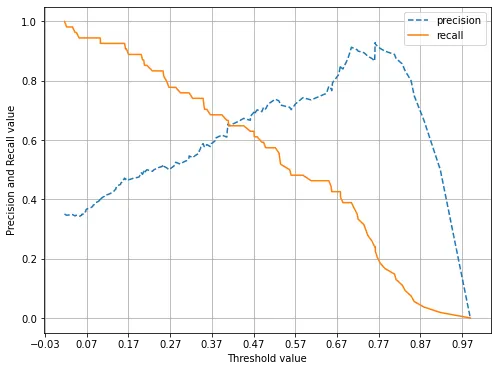
이를 위해, precision_recall_curve_plot() 함수를 이용해보자.
precision_recall_curve_plot(y_test,pred_proba)
Python
복사
대략 임계값을 0.42쯤으로 조정하면 정밀도와 재현율이 균형을 맞추는 것으로 확인된다. 하지만, 재현율과 정밀도 모두 0.7도 되지 않기 때문에 지표의 값이 충분하지 않다. 따라서, 원본 데이터의 분포를 다시 한번 확인해본다.
diabetes_data.describe()
Python
복사
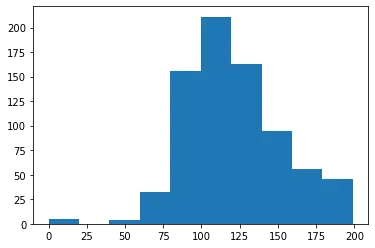
확인해보면, 많은 피처들의 min()값이 0인것을 확인할 수 있다. 하지만, 수치가 0인 것은 말이 되지 않는다. 따라서, 피처들의 히스토그램을 확인해보자.
plt.hist(diabetes_data['Glucose'],bins=10)
Python
복사
나머지 피처들도 확인해본다.
# 0값을 검사할 피처 명 리스트
zero_features = ['Glucose','BloodPressure','SkinThickness','Insulin','BMI']
# 전체 데이터 건수
total_count = diabetes_data['Glucose'].count()
# 피처별로 반복하면서 데이터 값이 0인 데이터 건수를 추출하고, 퍼센트 계산
for feature in zero_features:
zero_count = diabetes_data[diabetes_data[feature]==0][feature].count()
print('{0} 0 건수는 {1}, 퍼센트는 {2:.2f} %'.format(feature,zero_count,100*zero_count/total_count))
'''
Glucose 0 건수는 5, 퍼센트는 0.65 %
BloodPressure 0 건수는 35, 퍼센트는 4.56 %
SkinThickness 0 건수는 227, 퍼센트는 29.56 %
Insulin 0 건수는 374, 퍼센트는 48.70 %
BMI 0 건수는 11, 퍼센트는 1.43 %
'''
Python
복사
SkinThickness와 Insulin은 매우 높다. 따라서 이 값을 평균으로 대체하겠다.
# zero_features 리스트 내부에 저장된 개별 피처들에 대해서 0값을 평균 값으로 대체
mean_zero_features = diabetes_data[zero_features].mean()
diabetes_data[zero_features] = diabetes_data[zero_features].replace(0,mean_zero_features)
Python
복사
이렇게, 나름 이상치라고 할 수 있는 값을 잘 조정해줬고, 다음으로는 피처 스케일링을 해보겠다.
전체 데이터에 피처스케일링을 한 뒤, 학습/테스트 데이터로 나누겠다.
X = diabetes_data.iloc[:,:-1]
y = diabetes_data.iloc[:,-1]
# StandardScaler 클래스를 이용해서 피처 데이터 세트에 일괄적으로 스케일링 적용
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_train,X_test,y_train,y_test = train_test_split(X_scaled,y,test_size=0.2,random_state=156,stratify=y)
# 로지스틱 회귀로 학습, 예측, 평가 수행
lr_clf = LogisticRegression()
lr_clf.fit(X_train,y_train)
pred = lr_clf.predict(X_test)
pred_proba = lr_clf.predict_proba(X_test)[:,1]
get_clf_eval(y_test,pred,pred_proba)
'''
오차 행렬
[[90 10]
[21 33]]
정확도:0.7987, 정밀도:0.7674, 재현율:0.6111, f1 스코어:0.6804, AUC : 0.8433
'''
Python
복사
정밀도가 0.76, 재현율은 0.61로 어느 정도 성능 수치가 향상 되었다. 하지만, 여전히 재현율 수치는 개선이 확실히 필요해보인다.
이제부터는, 임계값을 변화시키면서 재현율 값의 성능 수치가 어느 정도나 개선되는지 확인해보자.
0.3에서 0.5까지 0.03씩 변화시키보자. 앞에서 만든 get_eval_by_threshold() 함수를 사용하자.
thresholds = [0.3,0.33,0.36,0.39,0.42,0.45,0.48,0.5]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test,pred_proba[:,1].reshape(-1,1),thresholds)
Python
복사
결과를 확인해보면 임곗값을 0.48로 결정하는 것이 전반적으로 모두 괜찮은 것 같다.
이제, 임곗값을 0.48로 낮춘 상태에서 다시 예측을 해보자. 단, 사이킷런의 predict() 메서드는 임곗값을 임의로 설정할 수 없다. 별도의 로직으로 이를 구해야 한다. Binarizer 클래스를 활용하자.
# 임곗값을 0.48로 설정한 Binarizer 생성
binarizer = Binarizer(threshold=0.48)
# 위에서 구한 lr_clf의 predict_proba() 예측 확률 array에서 1에 해당하는 칼럼값을 Binarizer 변환.
pred_th_048 = binarizer.fit_transform(pred_proba[:,1].reshape(-1,1))
get_clf_eval(y_test,pred_th_048,pred_proba[:,1])
'''
오차 행렬
[[88 12]
[19 35]]
정확도:0.7987, 정밀도:0.7447, 재현율:0.6481, f1 스코어:0.6931, AUC : 0.8433
'''
Python
복사