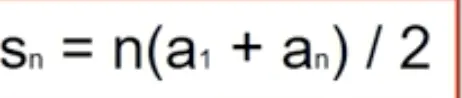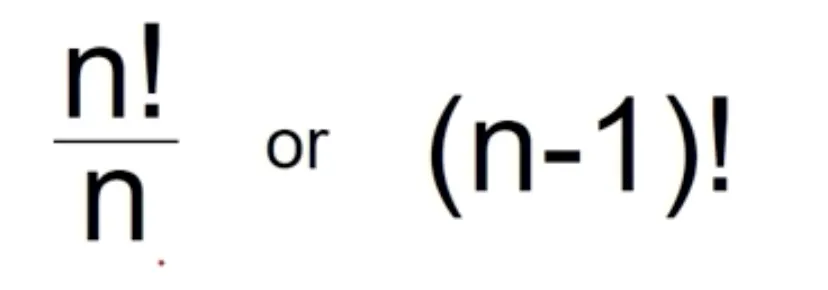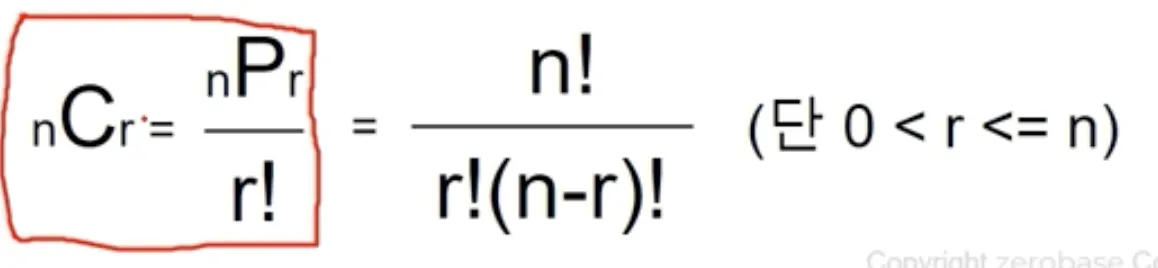기초 수학

약수 / 소수

# 사용자가 입력한 숫자의 약수를 출력
inputNum = int(input('0보다 큰 정수 입력: '))

for i in range(1, (inputNum + 1)):
    if inputNum % i == 0: # 나눠떨어지면 약수
        print(f'{inputNum}의 약수: {i}')
Python
복사

# 사용자가 입력한 숫자까지의 소수 찾기
inputNum = int(input('0보다 큰 정수 입력: '))

for num in range(2,(inputNum + 1)):
    flag = True
    for n in range(2,num):
        if num % n == 0:
            flag = False
            break

    if flag:
        print(f'{num}: 소수!')
    else:
        print(f'{num}: 합성수!')
Python
복사

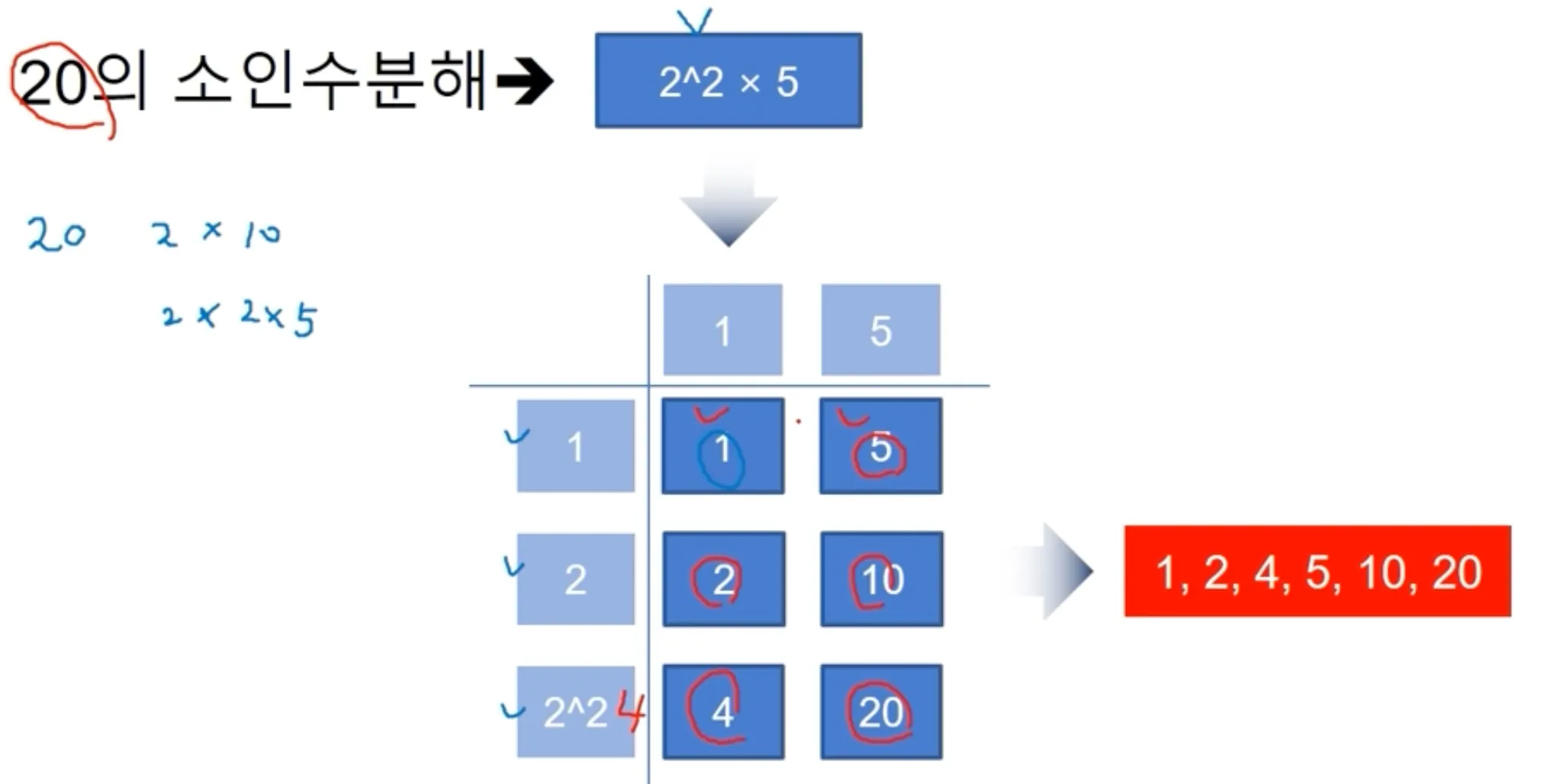
소인수분해

말 그대로, 소인수 : 소수 + 약수라서

약수 중에서 소수인 숫자를 소인수라고 보면 된다. 

따라서 소인수 분해는

어떤 수를 소인수로 분해하는 것을 말한다.

❗️소인수분해를 이용해서 약수를 정확하고 쉽게 구할 수 있다.

# 입력한 수를 소인수분해하자.
inputNum = int(input('1보다 큰 정수 입력: '))

n = 2
while n <= inputNum:
    if inputNum % n == 0:
        print(f'소인수 : {n}')
        inputNum /= n
    else:
        n += 1
Python
복사

# 72에 x를 곱하면 y의 제곱이 된다고 할 때, x에 해당하는 가장 작은 정수를 구하자.

inputNum = int(input('1보다 큰 정수 입력: '))

n = 2
numlist = []
while n <= inputNum:
    if inputNum % n == 0:
        print(f'소인수 : {n}')
        if numlist.count(n) == 0: # numlist 에 없고, 처음 나왔다면
            numlist.append(n)
        elif numlist.count(n) == 1: # 이미 들어있기 때문에, 그냥 신경쓸 필요 없다. -> 제거하자
            numlist.remove(n)

        inputNum /= n
    else:
        n += 1

print(f'searchNumber : {numlist}')
Python
복사

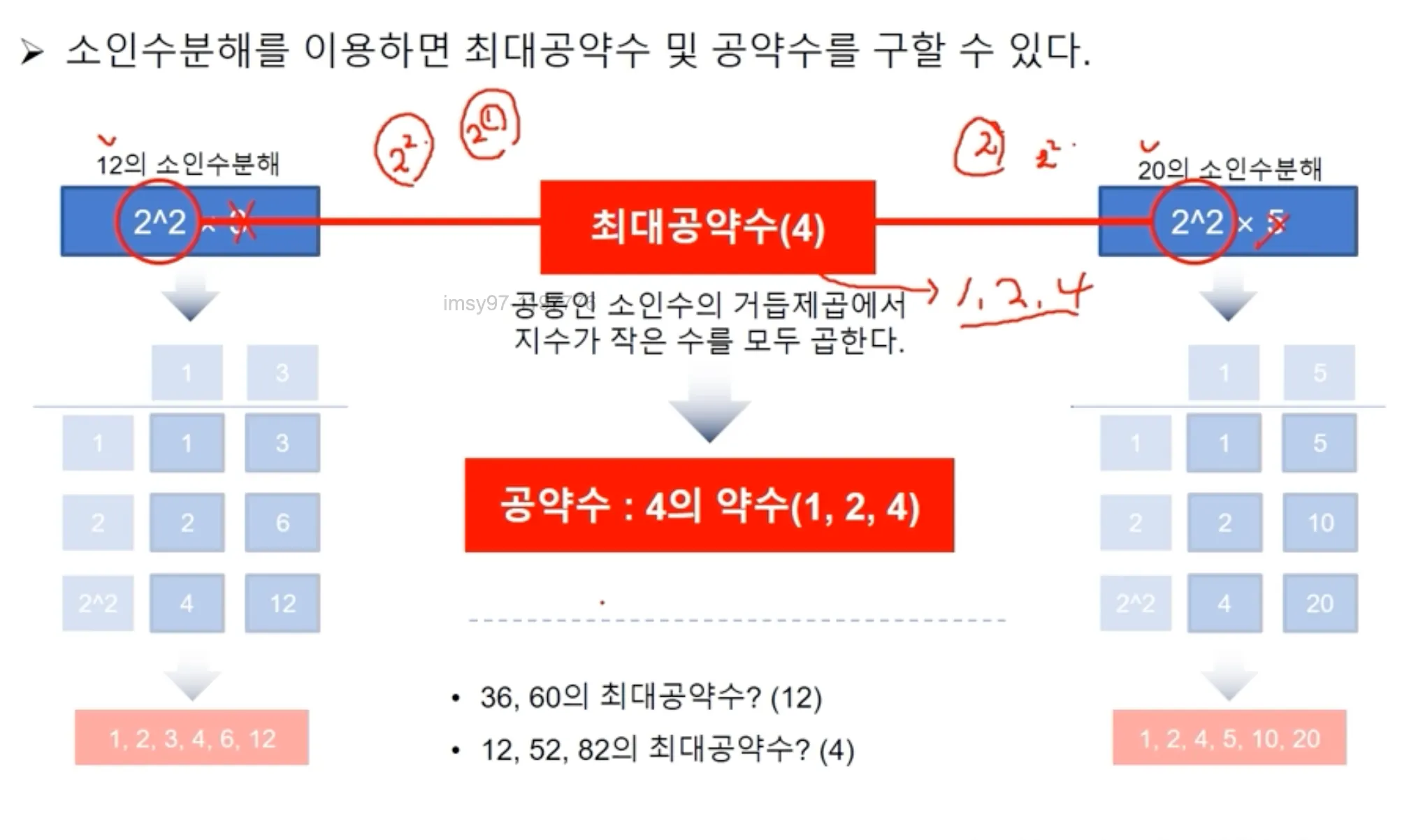
최대공약수

소인수분해를 이용하면 최대공약수 및 공약수를 구할 수 있다.

# 두 개의 수를 입력하면 공약수와 최대공약수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))

max_num = 0
for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        print(f'공약수 : {i}')
        max_num = i

print(f'최대공약수 : {max_num}')
Python
복사

# 세 개의 수를 입력하면 공약수와 최대공약수를 출력하는 코드
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
n3 = int(input('1보다 큰 정수 입력: '))

maxNum = 0
for i in range(1,(n1 + 1)):
    if n1 % i == 0 and n2 % i == 0 and n3 % i == 0: # 세 값에 모두 나눠떨어지면 공약수
        print(f'공약수 : {i}')
        maxNum = i
print(f'최대공약수 : {maxNum}')
Python
복사

유클리드 호제법

유클리드 호제법을 이용해서 최대공약수를 구할 수 있다.

•

x, y의 최대공약수는 y와 (x%y) 의 최대공약수와 같다.

n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))

temp1 = n1
temp2 = n2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print(f'{n1},{n2}의 최대공약수:  {temp1}')


# 최대공약수를 가지고 공약수를 구하기
for n in range(1,(temp1 + 1)):
    if temp1 % n == 0:
        print(f'{n1}, {n2}의 공약수 : {n}')
Python
복사

최소공배수

•

최대공약수를 이용해서 최소공배수 구하기

# 두 개의 수를 입력하면 최소공배수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        print(f'공약수 : {i}')
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (n1 * n2) // maxNum # 최소공배수
print(f'최소공배수: {minNum}')
Python
복사

# 세 개의 수를 입력하면 최소공배수를 출력하는 코드를 작성하자.
n1 = int(input('1보다 큰 정수 입력: '))
n2 = int(input('1보다 큰 정수 입력: '))
n3 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (n1 + 1)):
    if n1 % i == 0 and n2 % i == 0:
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (n1 * n2) // maxNum # 최소공배수
print(f'{n1}, {n2}의 최소공배수: {minNum}')

newNum = minNum
for i in range(1, (newNum + 1)):
    if newNum % i == 0 and n3 % i == 0:
        maxNum = i

print(f'최대공약수: {maxNum}')

minNum = (newNum * n3) // maxNum # 최소공배수
print(f'{n1}, {n2}, {n3}의 최소공배수: {minNum}')
Python
복사

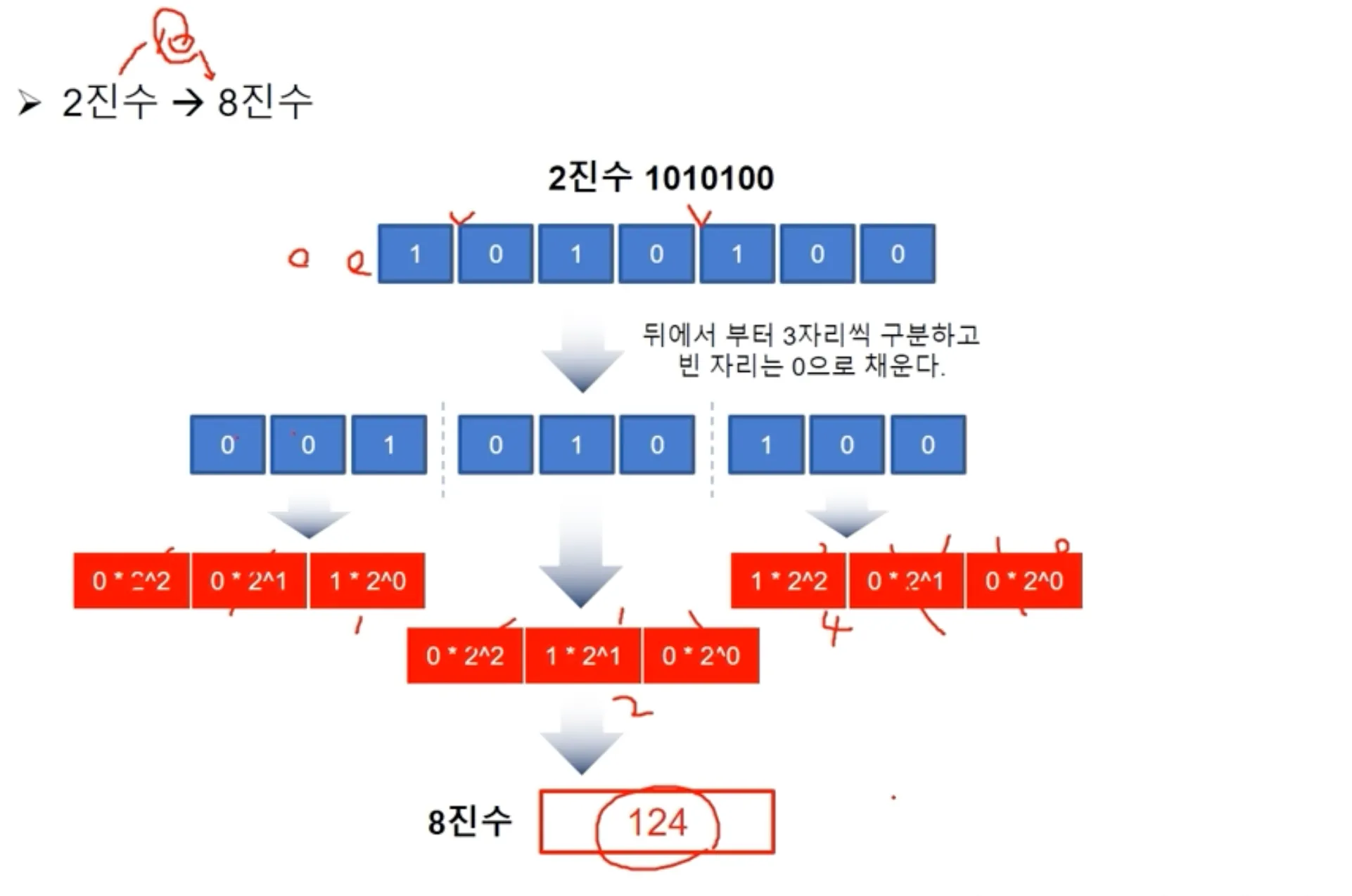
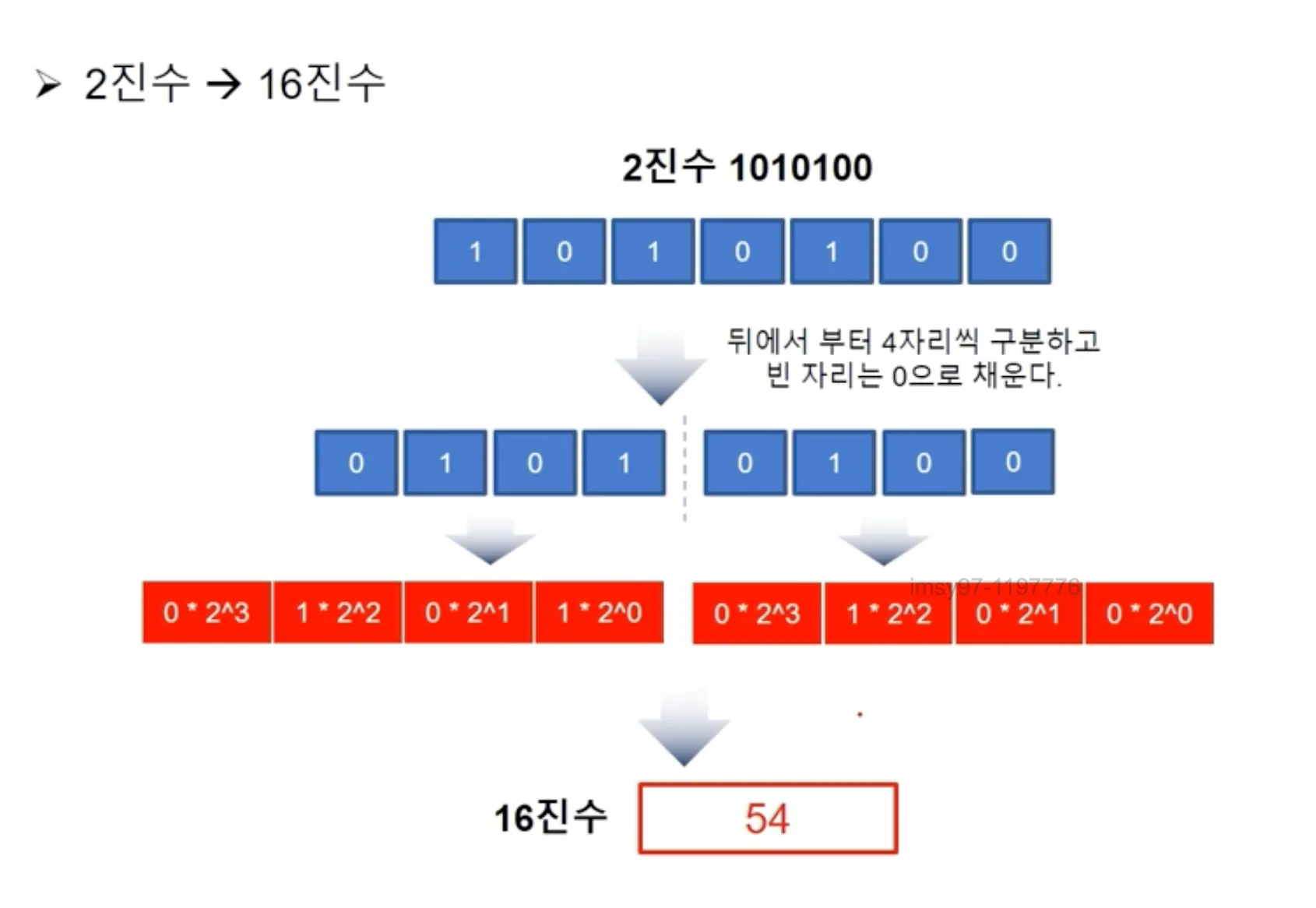
진법

•

2진수 → 8진수 변환

•

2진수 → 16진수

파이썬에서의 진법 변환

•

10진수 → 2진수, 8진수, 16진수 

◦

bin() : 2진수로 변환

◦

oct() : 8진수로 변환

◦

hex() : 16진수로 변환

•

이외에도 format() 함수로도 바꿀 수 있다.

dNum = 30
print('2진수: {}'.format(format(dNum, '#b'))) # 또는 '0b'를 빼고 출력하고 싶다면 'b' 만 써준다.
print('8진수: {}'.format(format(dNum, '#o'))) # 또는 'o'
print('16진수: {}'.format(format(dNum, '#x'))) # 또는 'x'


# 또는 아래와 같이 사용할 수도 있다.
print('{0:#b} , {0:#o},  {0:#x}'.format(dNum))
Python
복사

•

X진수 → 10진수

◦

int() 를 사용한다.  

•

X진수 → X진수

◦

8진수로 변환 : oct()

◦

2진수로 변환 : bin()

◦

16진수로 변환 : hex()

등차수열

# 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들자.

inputN1 = int(input('a1 입력: '))
inputD = int(input('d 입력: '))
inputN = int(input('n 입력: '))

n = 1
result = 0
while n <= inputN:
    # 항의 값을 구하기
    result = inputN1 + (n - 1) * inputD
    print(f'{n}번째 항의 값: {result}')
    n += 1
Python
복사

# 등차수열의 n번째 항까지의 합을 구하는 프로그램을 만들자.

inputN1 = int(input('a1 입력: '))
inputD = int(input('d 입력: '))
inputN = int(input('n 입력: '))

n = 1
while n <= inputN:
    # 첫째항과 끝항을 이용한 식으로 합을 구하자
    sum = (inputN1 + (inputN1 + inputD * (n - 1))) * n / 2
    print(f'{n}번째 항까지의 합: {int(sum)}')
    n += 1

Python
복사

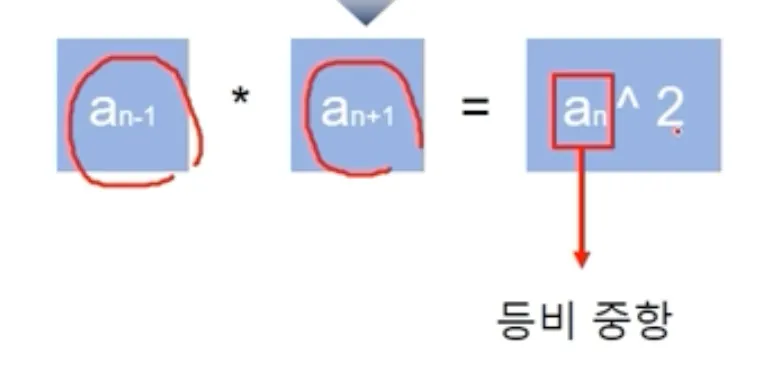
등비수열

# n번째 항의 값을 출력하는 프로그램. 등비수열

inputN1 = int(input('a1 입력: '))
inputR = int(input('r 입력: '))
inputN = int(input('n 입력: '))

n = 1
result = 1
while n <= inputN:
    result = inputN1 * inputR ** (n-1)
    print(f'{n}번째 항의 값: {result}')
    n += 1
Python
복사

# n번째 항까지의 합을 구하는 프로그램

inputN1 = int(input('a1 입력: '))
inputR = int(input('r 입력: '))
inputN = int(input('n 입력: '))

n = 1
result = 1
sum = 0
while n <= inputN:
    result = inputN1 * inputR ** (n-1) # n번째의 값
    sum += result
    print(f'{n}번째 항까지의 합: {sum}')
    n += 1


# 등비수열의 합을 구하는 공식 활용하는 방법
# n번째 항까지의 합을 구하는 프로그램

result = inputN1 * (1 - (inputR ** inputN)) / (1 - inputR)
print(f'{inputN}번째까지의 등비수열 합: {int(result)}')
Python
복사

시그마

생략

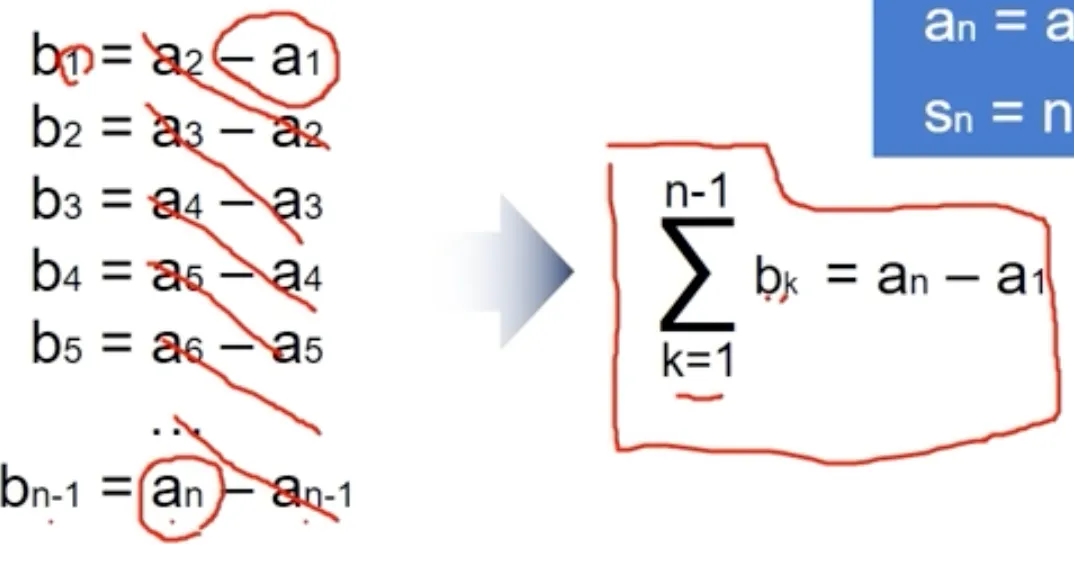
계차 수열

두 항의 차로 이루어진 수열

# 계차수열의 n번째 항의 값을 출력하는 프로그램을 만들어보자.

inputAn1 = int(input('a1 입력: '))
inputAn = int(input('an 입력: ')) # n번째 항

inputBn1 = int(input('b1 입력: '))
inputBD = int(input('bn 공차 입력: '))

valueAn = 0
valueBn = 0

n = 1
while n <= inputAn:

    if n == 1: # 1번째 항
        valueAn = inputAn1
        valueBn = inputBn1
        print(f'an의 1번째 항의 값: {valueAn}')
        print(f'bn의 1번째 항의 값: {valueBn}')
        n += 1
        continue

    valueAn = valueAn + valueBn
    valueBn = valueBn + inputBD
    print(f'an의 {n}번째 항의 값: {valueAn}')
    print(f'bn의 {n}번째 항의 값: {valueBn}')
    n += 1

print(f'an의 {inputAn}번째 항의 값: {valueAn}')
print(f'bn의 {inputAn - 1}번째 항의 값: {valueBn}')

# 계차수열 항 구하기
bn = inputBn1 + (inputAn-1) * inputBD
Python
복사

# bn의 n-1 항까지의 합 - a1 을 계산하면 an의 값을 구할 수 있다.

inputAn1 = int(input('a1 입력: '))
inputAn = int(input('an 입력: ')) # n번째 항

inputBn1 = int(input('b1 입력: '))
inputBD = int(input('bn 공차 입력: '))

# inputBn1 + inputBD * (inputAn - 1) # b(n-1) 의 값
sumBn = (inputBn1 + inputBD * (inputAn - 1) + inputBn1) * (inputAn - 1) / 2 # b(n-1)까지의 합
An = sumBn - inputAn1 # an

Python
복사

피보나치 수열

세번째 항은 첫번째 항과 두번째 항을 더한 값이다.

이때, 적어도 두항은 있어야 한다.

1,2번째 항은 1이어야 한다.

Python
복사

팩토리얼

•

반복문을 사용하는 경우

# 팩토리얼
# 1.반복문
inputN = int(input('n 입력: '))

result = 1
for i in range(inputN,0,-1):
    result *= i

print(f'{inputN} 팩토리얼: {result}')

# 또는
n = 1
result = 1
while n <= inputN:
		result *= n
		n += 1

print(f'{inputN} 팩토리얼: {result}')
Python
복사

•

재귀함수를 사용하는 경우

inputN = int(input('n 입력: '))

def factorialFun(n):
		if n == 1: return 1


		return n * factorialFun(n-1)

print(f'{inputN} 팩토리얼: {factorialFun(inputN)}')
Python
복사

# math 기능 활용하기 
import math

print(math.factorial(inputN))
Python
복사

군 수열 → 다시!!

여러 개의 항을 묶었을 때 규칙성을 가지는 수열

intputN = int(input('n항 입력: '))

flag = True
n = 1; nCnt = 1; searchN = 0 # nCnt 는 n항의 숫자를 담는 변수, searchN은 해당 항의 값을 담는 변수
while flag:
		
		for i in range(1, (n + 1)): # n은 군을 의미한다. 
				if i == n: 
						print('{} '.format(i), end='')
				else:
						print'{} ,'.format(i), end='')
				nCnt += 1
				
				if (nCnt > inputN):
						searchN = i
						flag = False
						break

		print()
		n += 1

print('{}항 : {}'.format(inputN, searchN))
Python
복사

# 분모값 따로, 분자값 따로 만들어줘야 한다.

inputN = int(input('n항 입력: '))

flag = True
n = 1; nCnt = 1; searchNC = 0; searchNP = 0
while flag:

    for i in range(1, (n + 1)): # 1 ~ n까지
        if i == n:
            print('{}/{} '.format(i, (n - i + 1)), end='')
        else:
            print('{}/{}, '.format(i, (n - i + 1)), end='')

        nCnt += 1
        if (nCnt > inputN):
            searchNC = i
            searchNP = n - i + 1
            flag = False
            break

    print()
    n += 1

print('{}항: {}/{}'.format(inputN, searchNC, searchNP))
Python
복사

순열 : nPr

순서를 지켜서 일렬로 나열하는 경우의 수

# 파이썬을 이용해서 순열을 구하는 프로그램
n = int(input('N 입력: '))
r = int(input('R 입력: '))

result = 1 #결과값 초기화
# nPr = n * (n-1) * ... * (n-r+1)

for i in range(n, (n-r), -1):
    result *= i

print('{}P{} 의 값 : {}'.format(n, r, result))
Python
복사

원순열

시작과 끝의 구분이 없는 순열

# n명의 사람이 원탁 테이블에 앉는 경우의 수를 구하자
# 1. math 모듈 활용
import math
n = int(input('친구 수 입력: '))
result = 1
print('{}명의 사람이 원탁에 앉는 경우의 수: {}'.format(n,math.factorial(n-1)))



# 2. 
n = int(input('친구 수 입력: '))
result = 1
for i in range(n-1, 0, -1): # 또는 range(1,n)
    result *= i
print('{}명의 사람이 원탁에 앉는 경우의 수: {}'.format(n,result))
Python
복사

조합

순서 상관없이 r개를 뽑는 경우

# 조합을 계산하는 프로그램을 만들자.
# 1. math
n = int(input('N 입력: '))
r = int(input('R 입력: '))
import math
result = 1

# nCr = n * ... * (n - r + 1) / r! -> (n - r)! / r!
result = (math.factorial(n) / math.factorial(n-r)) / math.factorial(r)
print('{}C{} 의 값: {}'.format(n,r,int(result)))
Python
복사

확률

모든 사건에서 특정 사건이 일어나는 경우의 수

조합을 이용해서 확률을 알아낼 수 있다.

import math
# 꽝이 4개, 선물이 3개 중에서 꽝 2개, 선물 1개를 뽑는 확률을 구하자.

while True:
    n = int(input('전체 카드 수 입력: '))
    r = int(input('뽑을 카드 수 입력: '))

    tot_case = math.factorial(n) / math.factorial(n-r) / math.factorial(r)
    print('sample: {}'.format(int(tot_case)))

    fail_n = int(input('fail card count 입력: '))
    fail_r = int(input('fail get count 입력: '))
    fail_case = math.factorial(fail_n) / math.factorial(fail_n - fail_r) / math.factorial(fail_r)
    print('event1: {}'.format(int(fail_case)))

    wow_n = int(input('wow card count 입력: '))
    wow_r = int(input('wow get count 입력: '))
    wow_case = math.factorial(wow_n) / math.factorial(wow_n - wow_r) / math.factorial(wow_r)
    print('event2: {}'.format(int(wow_case)))

    break
result = (fail_case * wow_case / tot_case) * 100
print('probability: {}%'.format(round(result,2)))
Python
복사