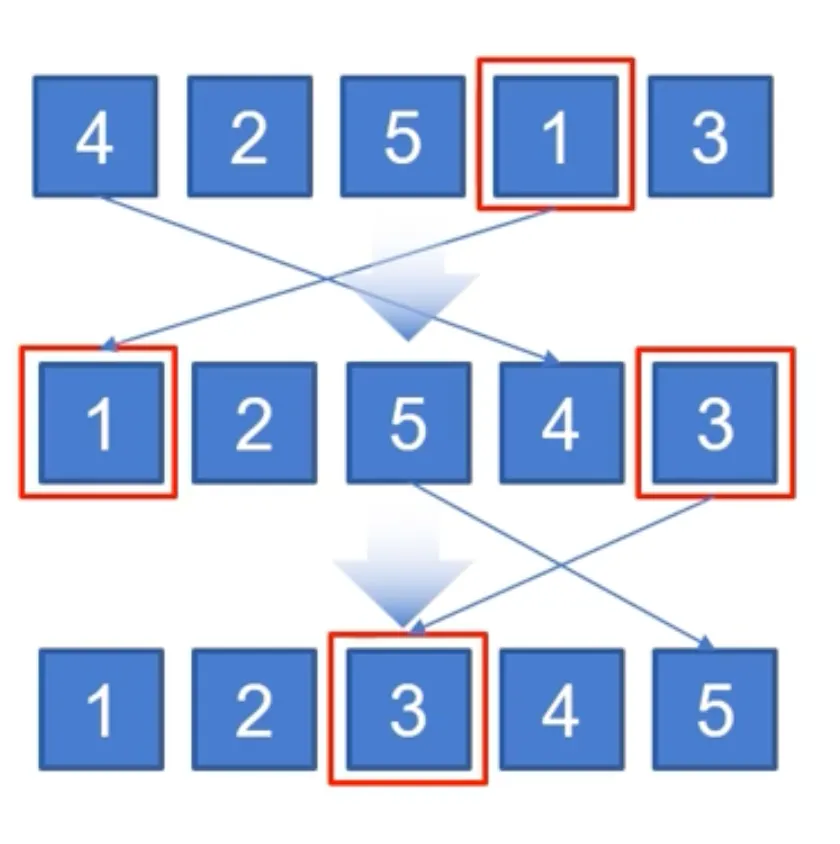
인덱스 0부터 시작해서 최솟값의 인덱스(위치)를 저장하고 맨 앞에 위치한 값(인덱스 0)과 최솟값을 교체하는 방식(1사이클)으로 자료를 정렬해가는 알고리즘이다.
중요한 점은 다음 사이클을 돌 때 최솟값이 들어온 이전의 인덱스 다음부터 확인해나간다는 점이다.
선택 정렬의 Big O 는 얼마일까? 크기 비교의 경우에는 버블 정렬과 동일하게 (N -1)번을 하게되지만, 스왑의 경우에는 매 싸이클마다 딱 1번씩만 교체하기 때문에 버블 정렬보다는 낫다.
하지만, 그럼에도 불구하고 Big O 는 N^2 다.
nums = [4,2,5,1,3]
print(f'nums : {nums}')
# nums 의 원소의 개수 - 1 의 횟수만 확인해주면 된다.
for i in range(len(nums)-1):
minIdx = i
# 최솟값의 인덱스를 찾아주는 과정
for j in range(i+1,len(nums)): # 최솟값을 찾아주기 위해서 비교할 원소들은 자기 자신 다음 인덱스부터 끝 인덱스까지다
if nums[minIdx] > nums[j]:
minIdx = j
# 최솟값을 지정해주고, swap 하는 과정
nums[i], nums[minIdx] = nums[minIdx], nums[i]
print(f'nums : {nums}')
Python
복사
# 시험점수 20개를 오름차순, 내림차순 정렬하는 프로그램
# 선택정렬 알고리즘을 사용하자
import random
stuScore = []
for _ in range(20):
stuScore.append(random.randint(50,100))
print(f'student Score : {stuScore}')
# 1. 오름차순
# 먼저, 19명의 점수 크기 비교만 진행해주면 된다.
for i in range(len(stuScore) - 1):
minIdx = i # 기준이 되는 인덱스를 설정해주고
# 최솟값의 인덱스를 설정해나가자 -> 최솟값 비교는 기준 i에서 그 다음 인덱스부터 끝까지 확인해주면 된다
for j in range(i+1, len(stuScore)):
if stuScore[minIdx] > stuScore[j]:
minIdx = j
# 최솟값의 위치 인덱스를 구했다면, 해당하는 최솟값과 i의 위치를 swap 한다.
stuScore[i], stuScore[minIdx] = stuScore[minIdx], stuScore[i]
print(f'sorted student Score : {stuScore}')
Python
복사
# 2. 내림차순
for i in range(len(stuScore) - 1):
maxIdx = i # 기준이 되는 인덱스를 설정해주고
# 내림차순 정렬은 기준되는 값보다 비교하는 값이 더 클 경우, swap 해주면 된다.
for j in range(i+1, len(stuScore)):
if stuScore[maxIdx] < stuScore[j]:
maxIdx = j
# 최솟값의 위치 인덱스를 구했다면, 해당하는 최솟값과 i의 위치를 swap 한다.
stuScore[i], stuScore[maxIdx] = stuScore[maxIdx], stuScore[i]
print(f'sorted descending student Score : {stuScore}')
Python
복사
# 모듈 이용해보자.
# choiceSort.py
def SortScore(ns, asc=True):
if asc: # 오름차순
for i in range(len(ns) - 1):
minIdx = i # 기준이 되는 인덱스를 설정해주고
# 최솟값의 인덱스를 설정해나가자 -> 최솟값 비교는 기준 i에서 그 다음 인덱스부터 끝까지 확인해주면 된다
for j in range(i + 1, len(ns)):
if ns[minIdx] > ns[j]:
minIdx = j
# 최솟값의 위치 인덱스를 구했다면, 해당하는 최솟값과 i의 위치를 swap 한다.
ns[i], ns[minIdx] = ns[minIdx], ns[i]
else: # 내림차순
for i in range(len(ns) - 1):
maxIdx = i # 기준이 되는 인덱스를 설정해주고
# 최솟값의 인덱스를 설정해나가자 -> 최솟값 비교는 기준 i에서 그 다음 인덱스부터 끝까지 확인해주면 된다
for j in range(i + 1, len(ns)):
if ns[maxIdx] < ns[j]:
maxIdx = j
# 최솟값의 위치 인덱스를 구했다면, 해당하는 최솟값과 i의 위치를 swap 한다.
ns[i], ns[maxIdx] = ns[maxIdx], ns[i]
return ns
Python
복사
import random
import choiceSort as cs
stuScore = []
for _ in range(20):
stuScore.append(random.randint(50,100))
print(f'student Score : {stuScore}')
print(f'ascending sorted score: {cs.SortScore(stuScore)}')
print(f'descending sorted score: {cs.SortScore(stuScore,False)}')
Python
복사
# 깊은 복사 활용하기 -> 기존 데이터 변형 안되기 위해
import random
import choiceSort as cs
import copy # 깊은 복사 사용
stuScore = []
for _ in range(20):
stuScore.append(random.randint(50,100))
print(f'student Score : {stuScore}')
result1 = cs.SortScore(copy.deepcopy(stuScore))
print(f'ascending sorted score: {result1}')
print(f'student Score : {stuScore}') # 정렬되기 전의 점수가 정렬된 것을 확인할 수 있다.
result2 = cs.SortScore(copy.deepcopy(stuScore), False)
print(f'descending sorted score: {result2}')
Python
복사
# 시험점수 20개를 오름차순, 내림차순 정렬하는 프로그램
# 선택정렬 알고리즘을 사용하자
# choiceSort.py
import copy
def selectNum(ns, asc=True):
c_ns = copy.copy(ns)
for i in range(len(ns) - 1): # swap은 전체 데이터 개수 -1 번만 해주면 된다.
minIdx = i # 최솟값의 인덱스를 저장할 변수를 첫번째값으로 지정해주고
# 최솟값의 인덱스를 구해보자. -> 최솟값 비교는 i + 1 인덱스부터 끝까지 확인해주면 된다
for j in range(i + 1, len(c_ns)):
if asc: # 오름차순
if c_ns[minIdx] > c_ns[j]: # 더 작은 값이 존재한다면
minIdx = j
else: # 내림차순
if c_ns[minIdx] < c_ns[j]: # 더 큰 값이 존재한다면
minIdx = j
# 최솟값의 위치 인덱스를 구했다면, 해당하는 최솟값과 i의 위치를 swap 한다.
c_ns[i], c_ns[minIdx] = c_ns[minIdx], c_ns[i]
print(f'nums : {c_ns}')
return c_ns
Python
복사
import random
import choiceSort
nums = random.sample(range(1,21),10)
print(f'not sorted nums :{nums}')
result = choiceSort.selectNum(nums)
print(f' sorted nums by asc : {result}')
result2 = choiceSort.selectNum(nums,False)
print(f' sorted nums by desc : {result2}')
Python
복사