피처 생성

기존의 피처들만으로 충분한 예측력을 발휘하지 못한다면 어떻게 할까?

이럴 때 필요한 것이 ‘피처 생성’ 이다.

기존 데이터에서 새로운 의미를 찾아내거나, 데이터의 관계를 재해석해서 새로운 피처를 만드는 과정이다.

Binning

어떤 상황에서 Binning 이 필요한가

실습

Scikit-learn 을 이용한 다항식 피처 생성

피처 중요도(feature importance)

Binning

연속적인 수치 데이터를 구간별로 범주화하는 기법

데이터의 세부적인 차이를 줄이고, 주요 패턴이나 경향성을 더 명확하게 파악할 수 있도록 한다.

어떤 상황에서 Binning 이 필요한가

•

이상치의 영향 감소

연속형 변수인 특정 feature에 극단적인 값이 다수 포함되어 있어 모델에 큰 영향을 미칠 가능성이 높다면, binning을 통해서 이런 이상치의 영향력을 완화시킬 수 있다.

•

비선형 패턴 포착

피처 변수와 타겟 변수 사이에 선형적인 관계 패턴이 보이지 않고 관계가 복잡할 때, Binning 기법은 두 데이터간의 숨겨진 비선형 관계를 드러내는 데 꽤 핵심적인 수단이 될 수 있다.

•

모델 해석의 용이성 및 변수간 관계의 단순화

실습

•

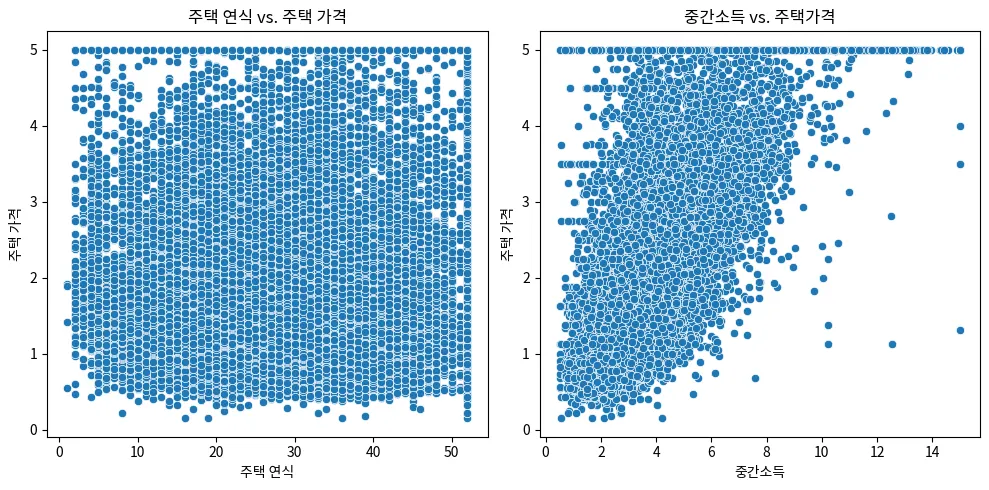
‘중간 소득’ - ‘주택 가격’ , ‘주택 연식’ - ‘주택 가격’ 의 관계를 알아보자.

◦

산점도

import pandas as pd
import seaborn as sns

housing_df = pd.read_csv('housing_california.csv')
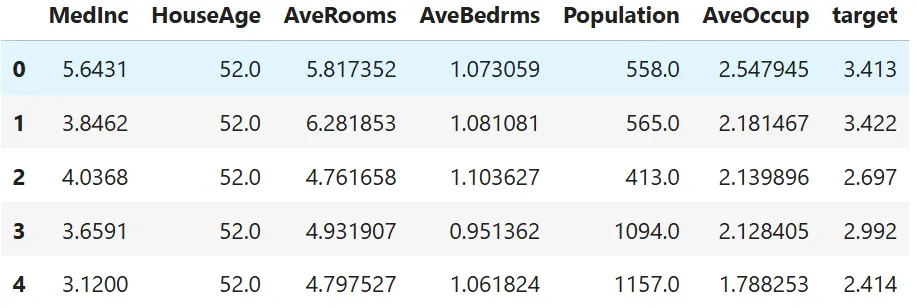
display(housing_df.head())
Python
복사

import matplotlib.pyplot as plt

fig, ax = plt.subplots(1,2, figsize=(10,5))

# HouseAge와 target 사이의 관계
sns.scatterplot(x=housing_df['HouseAge'], y=housing_df['target'], ax=ax[0])
ax[0].set_title('주택 연식 vs 주택 가격')
ax[0].set_xlabel('주택 연식')
ax[0].set_ylabel('주택 가격')

# MedInc와 target 사이의 관계
sns.scatterplot(x=housing_df['MedInc'], y=housing_df['target'], ax=ax[1])
ax[1].set_title('중간 소득 vs 주택 가격')
ax[1].set_xlabel('중간 소득')
ax[1].set_ylabel('주택 가격')

# 그래프간 충돌을 방지하기 위해 자동으로 레이아웃 조정
plt.tight_layout()
plt.show()
Python
복사

‘중간 소득’ 과 ‘주택 가격’ 사이에는 일정부분 선형 관계가 있음을 확인할 수 있다. 한편 ‘주택 연식’ 과 ‘주택 가격’ 사이에는 뚜렷한 패턴이 발견되지 않는다. → binning 을 통해 숨겨져 있는 패턴을 찾아볼 수 있다.

•

빈도 기반으로 범주화 하기 (Quantile-based Binning) - qcut

데이터를 분위수를 기준으로 동일한 빈도수를 가지는 구간으로 나누는 방법이다. 전체 데이터를 동등한 수의 관측치를 포함하는 그룹으로 나누고 싶을 때 사용된다.

데이터의 분포가 불균등할 때 유용하다

# '주택 연식' feature를 여섯개의 동일한 빈도수를 갖는 구간으로 범주화

# 등빈도 binning
housing_df['HouseAge_cat'] = pd.qcut(housing_df['HouseAge'], q=6)

# 생성된 범주 확인
HouseAge_cat = housing_df['HouseAge_cat'].value_counts().sort_index()
display(HouseAge_cat)
Python
복사

(0.999, 16.0]    4058
(16.0, 22.0]     3080
(22.0, 29.0]     3531
(29.0, 35.0]     3627
(35.0, 42.0]     3130
(42.0, 52.0]     3214
Name: HouseAge_cat, dtype: int64
Plain Text
복사

•

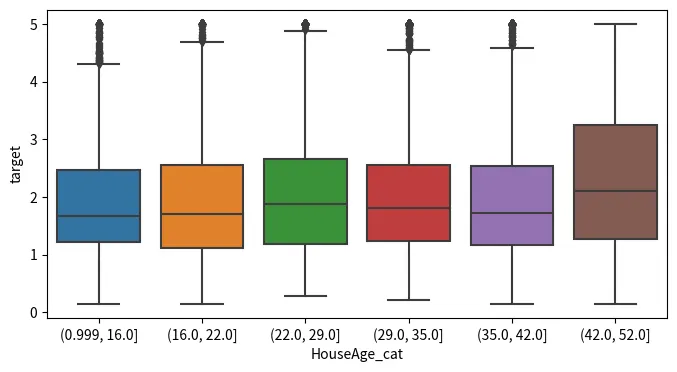
binning 통해 생성된 변수 시각화

# HouseAge_cat 과 주택 가격간의 관계를 boxplot 으로 시각화해보기

fig, ax = plt.subplots(figsize=(8,4))

# 상자 수염 그림 생성, 축(ax) 지정
sns.boxplot(x='HouseAge_cat', y='target', data=housing_df, ax=ax)

plt.show()
Python
복사

첫번째 범주에서는 다른 연령대의 집들과 크게 다르지 않게 target의 분포가 일정하게 유지가 되고 있는 것으로 보인다. 하지만, 이 범위의 이상치가 다른 범위보다 많이 보인다는 특징이 있다. 세번째 범주에서 중앙값이 증가하는 것을 볼 수 있는데, 이 전의 두 구간에 비해 target 값이 상승하는 경향이 있다는 것을 나타낸다. 다시 네번째 범주에서부터는 중앙값이 점진적으로 감소하는 경향을 보이고 있다.

다항식 피처 생성(Polynomial)

기존의 피처들을 사용해서 피처들의 고차항과 피처 간의 상호작용 항을 추가함으로써 새로운 피처 셋을 만드는 기법

피처들의 복잡한 패턴과 비선형 관계를 포착할 수 있는 정보를 얻을 수 있다.

import pandas as pd 
housing_df = pd.read_csv('californial_housing.csv')

housing_df['new_HouseAge_AveRooms'] = housing_df['HouseAge'] * housing_df['AveRooms']* housing_df['AveRooms']

features_analysis = ['HouseAge', 'AveRooms', 'new_HouseAge_AveRooms', 'target']
# 상관관계 행렬 계산
correlation_matrix = housing_df[features_analysis].corr()
print(correlation_matrix['target'])
Python
복사

HouseAge                 0.127987
AveRooms                 0.253044
new_HouseAge_AveRooms    0.311591
target                   1.000000
Name: target, dtype: float64
Plain Text
복사

import matplotlib.pyplot as plt
import seaborn as sns
fig, axs = plt.subplots(1,2, figsize=(12,6))

sns.regplot(x='AveRooms', y='target', data=housing_df, line_kws={'color':'red'}, ax=axs[0])
axs[0].set_title('AveRooms vs.Target')
axs[0].set_xlabel('AveRooms')
axs[0].set_ylabel('Target')
axs[0].set_xlim(0, 10)
axs[0].set_ylim(0, 5.2)

sns.regplot(x='new_HouseAge_AveRooms', y='target', data=housing_df, line_kws={'color':'red'}, ax=axs[1])
axs[1].set_title('new_HouseAge_AveRooms vs.Target')
axs[1].set_xlabel('new_HouseAge_AveRooms')
axs[1].set_ylabel('Target')
axs[1].set_xlim(0, 1000)
axs[1].set_ylim(0, 5.2)


plt.show()
Python
복사

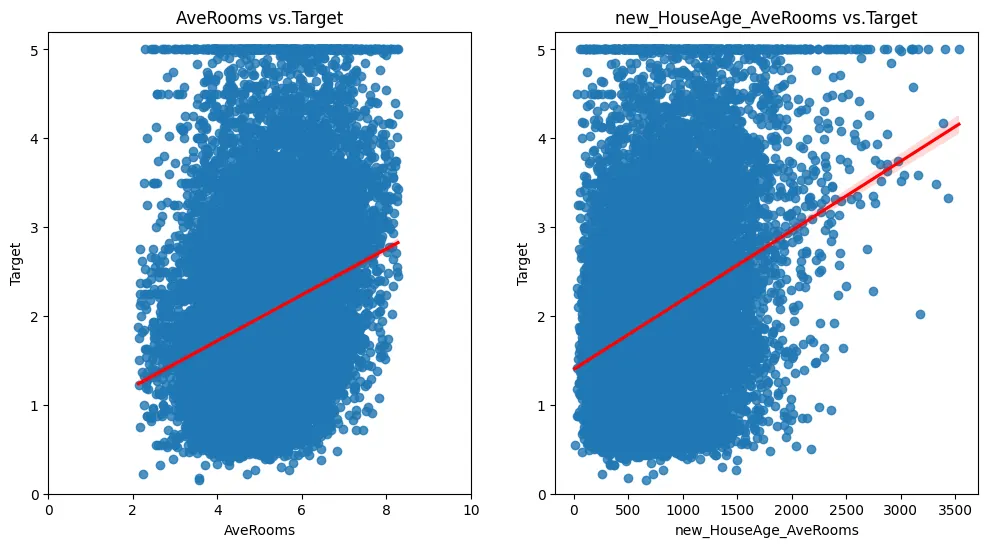
왼쪽 그래프의 경우에도 양의 상관관계를 보이지만, 다항식의 새로운 피처의 오른쪽 구간에서 새로운 패턴을 확인할 수 있다. → 이 구간에서는 확실히 평균 방의 개수가 많아질수록, 연식이 오래될수록 Target값도 높아지는 것으로 보인다.

AveRooms 단일 피처만으로는 포착하기 어려웠던 주택 연식과 방 개수의 상호작용 효과가 새로운 다항식 피처를 통해 나타난 것으로 보인다.

Scikit-learn 을 이용한 다항식 피처 생성

사이킷런의 PolynomialFeatures 변환기를 사용하면, 기존 피처의 다항식 조합을 쉽게 생성할 수 있다. 

# 라이브러리 import
from sklearn.preprocessing import PolynomialFeatures
import numpy as np


# 샘플 데이터 생성
X = np.arange(6).reshape(3,2)
print('Original features:\n', X)

# 다항식 피처 생성
poly = PolynomialFeatures(degree=2) # 2차 다항식
X_poly = poly.fit_transform(X)
print('Polynomial features:\n', X_poly) # 원본 피처 + 피처의 제곱 + 상호작용항
Python
복사

피처 생성 후에는 기존 변수들과의 상관관계를 분석해 불필요한 피처들을 제거해주어야 한다. 오히려 고차원의 피처들을 사용함으로써 모델 일반화 능력에 방해가 될 수도 있다. 마지막으로는 생성된 피처들을 사용했을 때의 교차검증 성능을 비교해서 실제로 긍정적인 영향을 미치는지도 확인해 주어야 한다. 차수(degree)를 너무 높게 설정하지 않도록 주의한다.

Polynomial 실습

import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
import numpy as np


train_solar = pd.read_csv('train_solar.csv')


train_solar_x = train_solar.drop(['ID', 'TARGET'], axis=1)

poly = PolynomialFeatures(degree=2, include_bias=False)

features_poly = poly.fit_transform(train_solar_x)
# get_feature_names_out 메소드 : 생성된 다항피처들의 이름
features_names = poly.get_feature_names_out(input_features=train_solar_x.columns)

# PolynomialFeatures로 생성된 피처들을 포함하는 새로운 DataFrame 생성
train_solar_poly_df = pd.DataFrame(features_poly, columns=features_names)
display(features_names)
display(train_solar_poly_df.head()) 
Python
복사

array(['DHI', 'DNI', 'WS', 'RH', 'T', 'DHI^2', 'DHI DNI', 'DHI WS', 'DHI RH', 'DHI T', 'DNI^2', 'DNI WS', 'DNI RH', 'DNI T', 'WS^2', 'WS RH', 'WS T', 'RH^2', 'RH T', 'T^2'], dtype=object)

	DHI	DNI	WS	RH	T	DHI^2	DHI DNI	DHI WS	DHI RH	DHI T	DNI^2	DNI WS	DNI RH	DNI T	WS^2	WS RH	WS T	RH^2	RH T	T^2
0	0.315650	0.885087	3.129167	-0.563454	-0.106409	0.099635	0.279378	0.987722	-0.177854	-0.033588	0.783379	2.769586	-0.498706	-0.094181	9.791684	-1.763142	-0.332971	0.317481	0.059956	0.011323
1	0.075239	0.756084	3.068750	-1.030301	0.317479	0.005661	0.056887	0.230889	-0.077519	0.023887	0.571663	2.320232	-0.778994	0.240041	9.417227	-3.161736	0.974263	1.061520	-0.327099	0.100793
2	0.148714	0.628092	1.547917	-1.190128	0.411156	0.022116	0.093406	0.230197	-0.176989	0.061145	0.394500	0.972235	-0.747511	0.258244	2.396046	-1.842219	0.636435	1.416405	-0.489328	0.169049
3	0.821308	0.283800	3.020833	-0.218049	1.308111	0.674547	0.233087	2.481034	-0.179085	1.074362	0.080542	0.857311	-0.061882	0.371241	9.125434	-0.658690	3.951585	0.047545	-0.285232	1.711155
4	0.174578	0.592866	2.056250	0.286934	-0.312498	0.030477	0.103501	0.358975	0.050092	-0.054555	0.351490	1.219080	0.170113	-0.185269	4.228164	0.590009	-0.642573	0.082331	-0.089666	0.097655

•

생성된 피처들과 Target 의 상관 분석

train_solar_poly_df['TARGET'] = train_solar['TARGET']

correlation_matrix = train_solar_poly_df.corr()
correlation_matrix['TARGET'].abs().sort_values(ascending=False)
Python
복사

TARGET     1.000000
DHI DNI    0.817730
DNI        0.726132
DNI^2      0.712234
T          0.689052
WS T       0.666005
DNI T      0.658100
DNI WS     0.554549
DHI T      0.513256
RH         0.486821
WS RH      0.479258
DNI RH     0.430429
DHI        0.346327
DHI RH     0.324267
DHI^2      0.299618
DHI WS     0.275917
WS^2       0.111976
WS         0.086688
RH^2       0.073187
T^2        0.055375
RH T       0.029028
Name: TARGET, dtype: float64
Plain Text
복사
- DNI 와 DHI 변수의 조합이 태양 에너지 출력에 중요한 비선형 영향을 미치는 것을 확인할 수 있다. → 즉, 두 변수의 상호작용이 태양 에너지 출력을 예측하는 데 핵심적인 역할을 한다는 걸 의미한다.

•

비선형 패턴 시각화(추가 분석)

•

피처 추가에 따른 모델 성능  평가(교차 검증)

피처 중요도(feature importance)

머신 러닝 모델 중에는 자체적으로 피처의 중요도를 계산하는 것들이 있다.

크게 두 가지 범주로 나눌 수 있는데, 

 - 트리 기반 모델
 - 선형 모델

•

트리 기반 모델 - 피처 중요도

데이터를 분류하거나 예측할 때 피처가 얼마나 유용한지를 평가

from sklearn.tree import DecisionTreeRegressor

housing_df = pd.read_csv('californial_housing.csv')
housing_df.head()
Python
복사

X = housing_df.drop('target', axis=1)
y = housing_df['target']

model_dt = DecisionTreeRegressor(random_state=42)
model_dt.fit(X, y)

# 피처 중요도 추출
feature_importances_dt = model_dt.feature_importances_
display(feature_importances_dt)

# feature_importances와 X.columns을 이용하여 중요도가 높은 순서로 정렬하여 출력

df_feature_importances_dt = pd.DataFrame({
												'Feature': X.columns,
												'Importance': feature_importances_dt})
sorted_df_feature_importances_dt = df_feature_importances_dt.sort_values(by='Importance', ascending=False).reset_index(drop=True)

display(sorted_df_feature_importances_dt)
Python
복사

array([0.47470085, 0.09667093, 0.09763334, 0.06455698, 0.06876249, 0.19767541])

	Feature	Importance
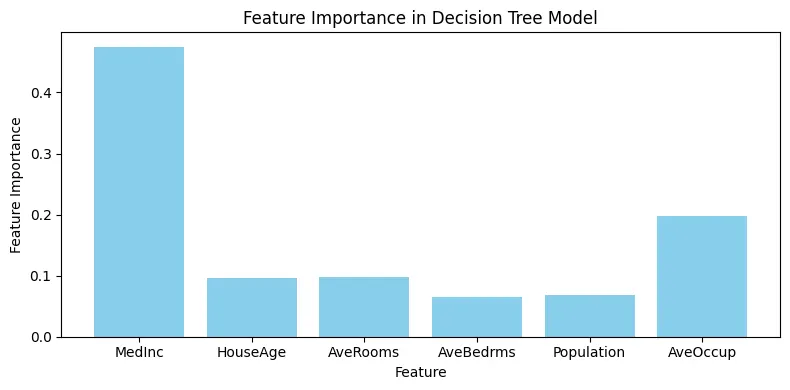
0	MedInc	0.474701
1	AveOccup	0.197675
2	AveRooms	0.097633
3	HouseAge	0.096671
4	Population	0.068762
5	AveBedrms	0.064557

# 피처 중요도 시각화
import matplotlib.pyplot as plt

# 피처 중요도를 수직 바 그래프로 시각화
fig, ax = plt.subplots(figsize=(8, 4))
ax.bar(X.columns, feature_importances_dt, color='skyblue')

ax.set_xlabel("Feature")
ax.set_ylabel("Feature Importance")
ax.set_title("Feature Importance in Decision Tree Model")

plt.tight_layout()  # 레이블이 잘리지 않도록 조정
plt.show()
Python
복사

•

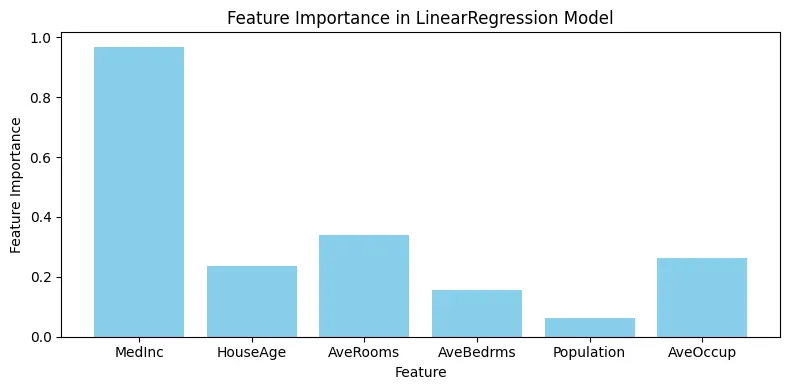
선형 모델 - 피처 중요도

각 피처에 할당된 가중치(회귀 계수)의 크기와 방향을 통해 중요도를 평가한다.

이때 선형 모델의 경우에는 반드시 피처 정규화를 진행해줘야 한다.

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

# 피처 스케일링
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 스케일링된 데이터로 선형 회귀 모델 학습
model_lr_scaled = LinearRegression()
model_lr_scaled.fit(X_scaled, y)

# 피처의 가중치를 피처 중요도로 사용 (스케일링된 모델)
feature_importances_lr = abs(model_lr_scaled.coef_)

feature_importances_lr
Python
복사

array([0.96849035, 0.23637448, 0.33845237, 0.15501547, 0.06306794,
       0.26386702])
Plain Text
복사

# 시각화
import matplotlib.pyplot as plt
# 피처 중요도를 수직 바 그래프로 시각화

fig, ax = plt.subplots(figsize=(8, 4))
ax.bar(X.columns, feature_importances_dt, color='skyblue')

ax.set_xlabel("Feature")
ax.set_ylabel("Feature Importance")
ax.set_title("Feature Importance in Decision Tree Model")

plt.tight_layout()  # 레이블이 잘리지 않도록 조정
plt.show()
Python
복사

•

통계 기반 피처 중요도

피처와 타겟 변수간의 관계를 수치적으로 평가한다.

가장 흔하게 ‘상관 계수’