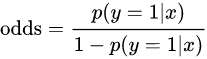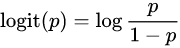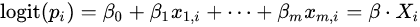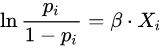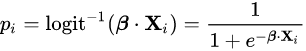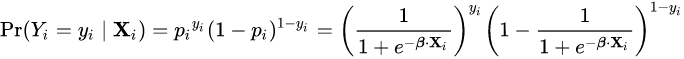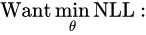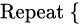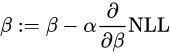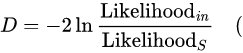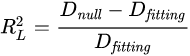Search

Logistic Regression

독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서는 선형 회귀 분석과 유사하다. 하지만 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류 기법으로도 볼 수 있다.
회귀와 분류 모두에 쓰인다.
모델의 가정은 종속변수 y가 이항분포를 따르며 그 모수 u가 설명변수 x에 의존한다.
로지스틱은 y가 특정 구간내의 값만 가질 수 있으므로 종속변수가 이런 특성을 가졌을 경우에 사용 가능하다.
이진분류일 경우, 로지스틱 회귀의 y는 0 또는 1의 값을 가진다. y가 다항 범주를 가지는 경우 다항 로지스틱 회귀라고 부르며 순서까지 있다면 서수 로지스틱 회귀다. 먼저 이진분류일 경우만 고려해보자.
일반적인 선형회귀와의 차이점은 다음과 같다.
•
이항형인 데이터에 적용했을 때 종속 변수 y가 범위 [0,1]로 제한된다.
•
종속변수 y가 정규분포가 아닌 이항분포를 따른다.
회귀문제일 경우 y의 예측값은 간단하게 설명변수들의 평균값이다.

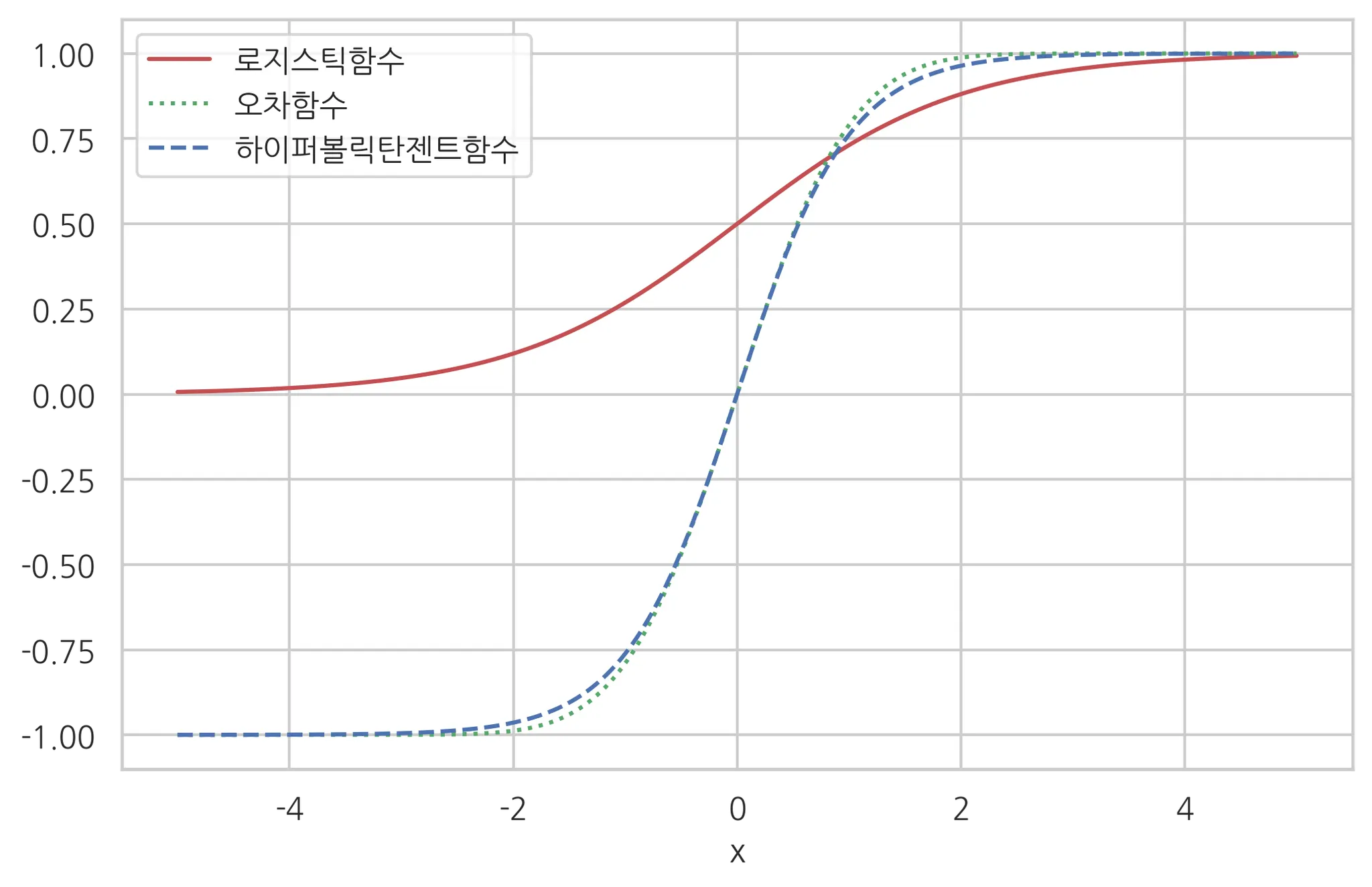
시그모이드 함수

이진분류일 경우 설명변수들의 평균인 u는 x의 함수라고 가정하고, 이 u(x)의 값을 0~1 사이의 값으로 변형하기 위해 사용하는 함수가 시그모이드 함수다.
시그모이드 함수는 아래 종류들이 있다.
•
로지스틱 함수
•
tanh
•
오차 함수
하지만 보통 시그모이드함수라고 하면 로지스틱함수를 가리킨다. 그 이유는 계산상의 편리성이다.
독립변수는 (−Inf,Inf)(-Inf,Inf) 즉, 아무값이나 입력되고 종속변수는 범위 [0,1] 사이에 있도록 한다. 이는 odds를 로짓변환을 수행하면서 얻어진 결과다.
오즈는 실패확률분에 성공확률이다.
로짓변환은 오즈에 로그변환을 취한 것이다. 따라서 출력값의 범위는 (−Inf,Inf)-Inf,Inf) 가 된다.
로지스틱 회귀에서 로짓 변환의 결과는 x에 대한 선형 함수와 동일하므로,
가 되고, 정리하면
가 된다.
따라서, 우리가 구하고자 하는 특정 독립 변수 x가 주어졌을 때, 종속 변수가 1의 카테고리에 속할 확률은 다음과 같다.
이를 확률 질량 함수로 표현하면 다음과 같다.

모델 적합

모델 적합에는 추정(estimation)과 추정의 결과를 평가(evaluation)하는 과정으로 나뉜다. 추정은 로지스틱 회귀를 통한 모델을 설정할 때 필요한 계수를 예측하기 위한 것이고, 평가는 추정한 모델이 데이터에 적합한지 판단하기 위한 것이다.

모델 적합 - 추정(estimation)

1.
최대 가능도 방법 (로그 우도)
•
최대 가능도 방법?
•
로그 가능도 우도
가능도 우도가 최대가 되는 값을 찾는 것은 결국 계수(베타)를 찾는 것이다. 이때, 편의상 가능도 함수를 그대로 사용하지 않고 로그를 취한 뒤, -를 붙인 함수 즉, Negative Log Likelihood를 사용한다.
이를 -LL 라고 부르는데 해당 값이 최소화 되는 계수를 추정한다고 보면 된다.
로지스틱 회귀에서는 위의 식을 최소화하는 닫힌 형태를 바로 구하는 것이 불가능하다. 그래서 반복 처리(iterative process)를 통해 계수를 추정하는데, 이 과정은 임의의 계수에서 시작하여 해당 계수를 반복적으로 수정해가면서 결과 모델이 개선되는지를 확인한다.
하지만 특정 경우에는 모델이 수렴하지 않을 수도 있는데, 이는 반복 처리로써 적합한 해를 찾을 수 없기 때문으로 계수가 중요한 의미를 지니지 않음을 시사한다. 수렴에 실패하는 대표적인 이유로는 사건에 매우 큰 영향력을 미치는 예측변수의 사용, 다중 공선성(multicolinearity), 희소성(sparseness), 완분성(complete separation)들이 있다.
•
경사 하강법
: 반복적으로 업데이트하면서 최솟값을 찾아내는 대표적인 알고리즘이다. -LL에 적용시키면 다음과 같다.

모델 적합 - 평가

다양한 방법이 사용된다. 대표적인 방법으로는 가능도비 검정, Walt test, Pseudo-R^2s, Hosmer-Lemeshow test가 존재한다.
•
가능도비 검정
두 개의 모형의 가능도비를 계산하여 두 모형의 가능도가 유의한 차이가 나는지를 비교함으로써 회귀 계수가 통계적으로 유의한지를 검정하는 방법이다.
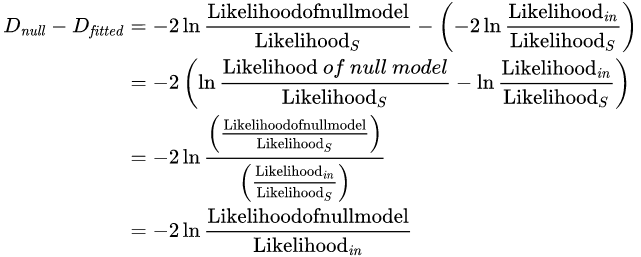
'포화 모델(이론적으로 완벽히 들어맞는 모델)'을 구할 수 있다고 했을 때, 편차값은 주어진 모델과 포화 모델을 비교함으로써 계산된다.
Likelihood(in) 은 적합된 모델을 가능도, Likelihood(s)는 포화 모델의 가능도, D는 편차값)
→ 가능도비에 자연로그를 취한 값은 음수이기 때문에 -2를 곱함으로써 근사적으로 카이제곱 분포를 따르게 만든다.
→ 편차값이 작을수록 포화모델과 차이가 적은, 잘 맞춰진 분석모델임을 의미한다.
로지스틱 회귀에서 편차를 측정하기 위한 또 다른 중요한 측정값은 널편차와 모델 편차이다. 널편차는 예측 모형이 적용되지 않은, 즉, 예측 변수가 없는 모델과 포화 모델간의 차이를 말한다. 이 때, 널편차는 예측 변수 모델과 비교할 대상의 기준을 제공한다. 편차값을 주어진 모델과 포화 모델 사이의 차이라고 가정했을 때, 두 모델간의 편차가 작을수록 오차가 적은 분석 모델이다.
따라서 예측 변수들의 기여도를 평가하기 위해, 널 편차값에서 모델 편차값을 빼거나, 예측할 매개변수의 개수 차이를 자유도로 가지는 카이제곱 분포(χs−p2)({\displaystyle \chi _{\mathit {s-p}}^{2}} )로 나타낼 수 있다. 그리고 이를 기준으로 F-test를 수행함으로써 최종적으로 회귀 계수의 유의성을 판단할 수 있다.
•
의사 결정계수(Pseudo-R2)
R2R^2를 계산하는 방법은 통일되어 있지 않고 많은 방법이 존재하는데, 이들 중 대표적인 세 가지는 McFadden (1974)가 제안한 방법, Cox and Snell (1989)가 제안한 방법, 그리고 Cox and Snell R2R^2 의 수정 버전이 존재한다. 범위는 [0,1]
McFadden이 제안한 R2R^2은 의사-결정계수라고도 불리는데, 이는 다음과 같이 정의된다.
pseudo-R2R^2의 단점은 오즈비와 직접적으로(monotonically) 연관되어 있지 않다는 점이다.
•
Cox and Snell R2R^2
선형 회귀 분석과 동일한 원리를 이용하는 것으로서, 선형 회귀 분석에서의 일반적인R2 R^2 이 이 공식에 의해 예측 변수가 없는 모델과 있는 모델의 가능도로 결정된다. 이것의 장점은 최대 가능도 추정을 하는 다른 종류의 회귀 분석으로 확장될 수 있다는 것이다. 하지만 Cox and Snell이 제안한 결정계수는 최대 값이 1.0보다 작고, 특정 경우에는 1.0에 비해 상당히 작은 값이 될 수도 있다는 단점이 존재한다.
→ 의사-결정계수가 Cox and Snell이 제안한 결정계수에 비해 조금 더 선호되는 경향이 있는데, 그 이유는 선형 회귀의 결정계수와 가장 유사하고, 기저율(base rate)에 독립적이기 때문이다. 또한 CoX and Snell이 제안한 R2R^2과는 달리 이는 범위 [0,1]을 가진다.
→ 의사-결정계수를 이용한 해석에서의 유의점은 선형분석에서의 R2R^2 해석과 다르다는 것이다.
→ 로지스틱 회귀분석은 종속 변수가 범주형이므로 오차의 등분산성 가정이 만족되지 않고, 따라서 오차 분산이 예측된 확률에 따라 달라진다. 또한 로지스틱 회귀분석에서 R2R^2 은 대개 낮게 나오는 편이므로, 모델 평가에서 R2R^2에 너무 의존할 필요는 없다.

StatsModels 패키지의 로지스틱 함수

StatsModels 패키지는 베르누이 분포를 따르는 로지스틱 회귀 모형 Logit을 제공한다. 종속변수와 독립변수 데이터를 넣어모형을 만들고 fit메서드로 학습한다.
fit메서드의 disp=0은 최적화 과정에서 문자열 메세지를 나타내지 않는 역할이다.
from sklearn.datasets import make_classification from statsmodels.api as sm # 독립변수 1개 X0, y = make_classification(n_features=1, n_redundant=0, n_informative=1, n_clusters_per_class=1, random_state=4) X = sm.add_constant(X0) # 상수 추가 logit_mod = sm.Logit(y,X) logit_res = logit_mod.fit(disp=0) print(logit_res.summary()) # 임의의 값 넣어 예측하기 xx = np.linspace(-3,3,100) mu = logit_res.predict(sm.add_constant(xx))
Python
복사

판별함수

Logit 모형의 결과 객체에는(logit_res) fittedvalues라는 속성으로 판별함수 값이 들어있다.
scikit-learn 패키지의 metrics 서브패키지에는 로그 손실을 계산하는 log_loss 함수가 존재하는데, normalize=False로 설정하면 이탈도와 같은 값을 구해준다.
from sklearn.metrics import log_loss y_hat = logit_res.predict(X) log_loss(y,y_hat,normalize=False)
Python
복사
대략 로지스틱 모델의 로그 손실이 16.08로 계산된다고 한다.
null model의 yhat 값을구해서 로그 손실을 비교해보면
mu_null = np.sum(y)/len(y) -- null_model의 y평균값 y_null = np.ones_like(y)*mu_null -- null_model의 yhat log_loss(y,y_null,normalize=False)
Python
복사
대략 69라는 값이 나온다.
이제, 두 값을 이용해서 맥파든 의사결정계수값을 구하면 끝이다.
1 - (log_loss(y,y_hat)/log_loss(y,y_null))
Python
복사

Scikit-Learn 패키지의 로지스틱 회귀

사이킷런 패키지는 로지스틱 회귀 모형 LogisticRegression 을 제공한다.
from sklearn.linear_model import LogisticRegression model_sk = LogisticRegression().fit(X0,y) xx = np.linspace(-3,3,100) # 임의의값 xx 생성
Python
복사

붓꽃 분류 문제에서의 로지스틱 활용

세토사(y=0) 와 베르시칼라(y=1)을 분류하는 이진분류문제에서 독립변수는 꽃받침길이와 상수를 사용한다.
1.
먼저 StatsModels 패키지를 사용해서 구해보자.
from sklearn.datasets import load_iris iris = load_iris() X = iris.data y = iris.target dfX = pd.DataFrame(X,columns=iris.feature_names) dfy = pd.DataFrame(y,columns=['species']) df = pd.concat([dfX,dfy],axis=1) df = df[['sepal length (cm)','species']] df = df[df.species.isin([0,1])] # setosa와 versicolor 데이터만 뽑기 df = df.rename(columns={'sepal length (cm)':'sepal_length'}) import statsmodels.api as sm model = sm.Logit.from_formula('species ~ sepal_length', data=df) # 모델 객체 생성 result = model.fit() print(result.summary())
Python
복사
statsmodels의 기준값(threshold)은 다음과 같이 구한다.
# 기준값 (0.5 + intercept값) / x1회귀계수값
Python
복사
predict함수를 사용해서 예측결과를 구할 수 있는데, 이때 예측결과값은 1이 될 확률이다.
따라서 임곗값에 따라서 분류를 해줘야 하는데, 일단 기본적인 0.5로 해본다.
y_pred = result.predict(df.sepal_length) >= 0.5 # 즉 1이 될 확률이 0.5이상인 값들은 True, 작으면 False로 변환 # 테스트데이터의 예측성능을 평가해보자. from sklearn.metrics import confusion_matrix confusion_matrix(df.species,y_pred) precision recall f1-score support 0 0.88 0.90 0.89 50 1 0.90 0.88 0.89 50 accuracy 0.89 100 macro avg 0.89 0.89 0.89 100 weighted avg 0.89 0.89 0.89 100 # 정확도, 정밀도, f1-score, 재현율 값을 모두 확인해본다. from sklearn.metrics import classification_report print(classification_report(df.species,y_pred)) # roc curve 도 확인해본다. 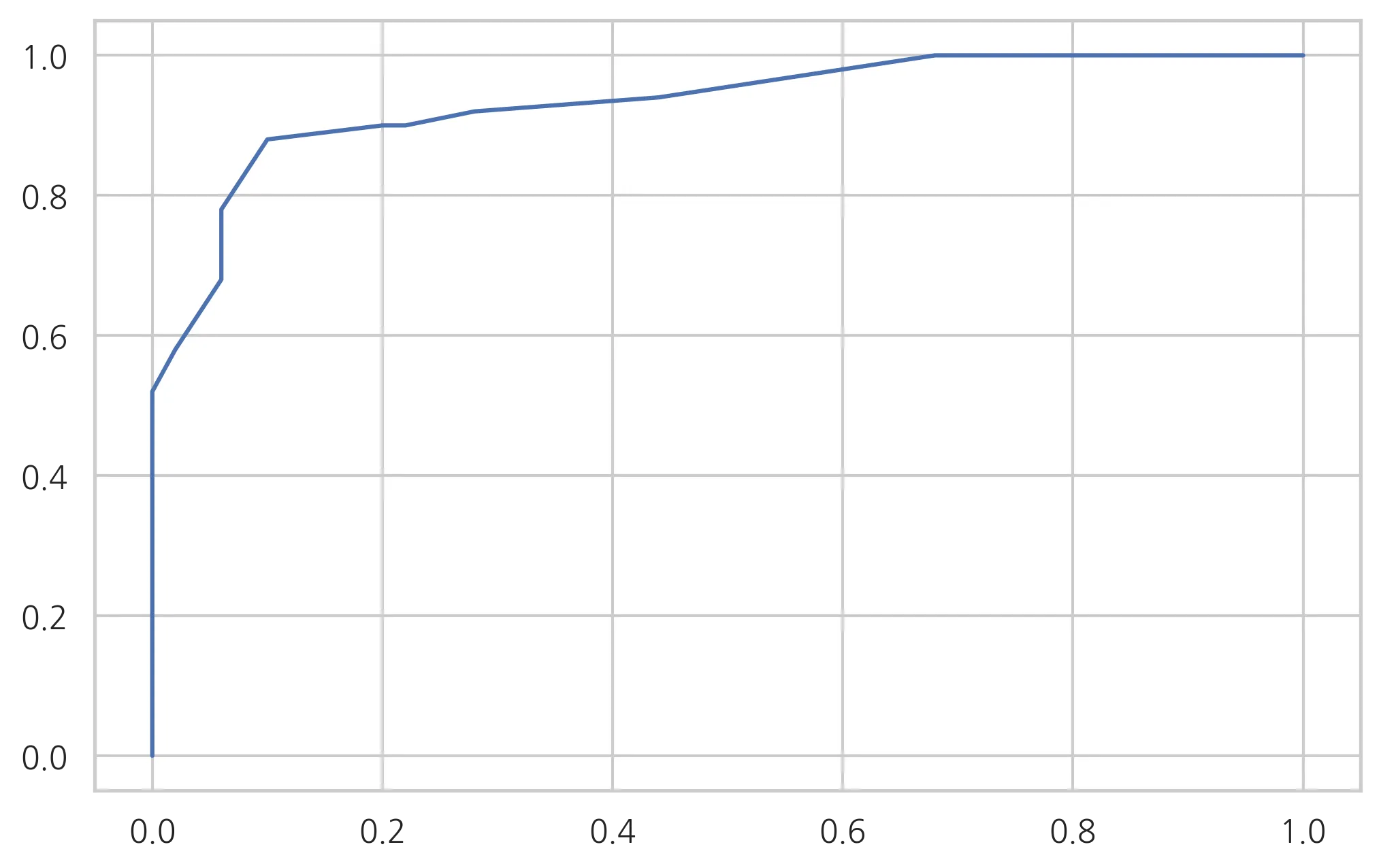from sklearn.metrics import roc_curve fpr, tpr, thresholds = roc_curve(df.species, result.predict(df.sepal_length)) # roc커브는 레이블값에 대한 원본확률값을 입력해준다. plt.plot(fpr,tpr) plt.show()
Python
복사
마지막으로 auc값도 확인한다.
from sklearn.metrics import auc auc(fpr,tpr) 0.9326
Python
복사
기준모델(null model)은 무조건 레이블을 train의 y 최빈클래스로 예측하는 것이다. 기준모델의 정확도를 확인해보려면 다음과 같이 한다.
# null model # 일단, 위의 문제에서는 train과 test를 나누지 않았으므로 그냥 y의 최빈값이라고 생각한다. majority_class = dfy.mode()[0] # null모델의 정확도 계산을 위해 데이터 생성 y_pred = [majority_class] * len(df) # 정확도 확인 print('null model의 정확도 : ', accuracy_score(df.species,y_pred))
Python
복사
적어도 null model의 정확도보다는 높게 나와야 의미가 있는 모델이라고 할 수 있다.
이번에는, versicolor(=1) 와 virginica(=2)를 분류해보자. 이때, 독립변수는 이번에 다 쓰도록 한다. 또한, 이 버지니카와 베르시칼라를 구분하는 경계면의 방정식도 구해보자.
df = df[df.species.isin([1,2]) df['Species'] -= 1 # versicolor를 0, virginica를 1로 바꾼다. df = df.rename( columns={ 'sepal length (cm)':'sepal_length', 'sepal width (cm)':'sepal_width', 'petal length (cm)':'petal_length', 'petal width (cm)':'petal_width' } ) import statsmodels.api as sm model = sm.Logit.from_formula('Species ~ sepal_length+sepal_width+petal_length+petal_width', data=df) result = model.fit() print(result.summary()) Optimization terminated successfully. Current function value: 0.059493 Iterations 12 Logit Regression Results ============================================================================== Dep. Variable: species No. Observations: 100 Model: Logit Df Residuals: 95 Method: MLE Df Model: 4 Date: Sat, 06 Jun 2020 Pseudo R-squ.: 0.9142 Time: 10:01:37 Log-Likelihood: -5.9493 converged: True LL-Null: -69.315 Covariance Type: nonrobust LLR p-value: 1.947e-26 ================================================================================ coef std err z P>|z| [0.025 0.975] -------------------------------------------------------------------------------- Intercept -42.6378 25.708 -1.659 0.097 -93.024 7.748 sepal_length -2.4652 2.394 -1.030 0.303 -7.158 2.228 sepal_width -6.6809 4.480 -1.491 0.136 -15.461 2.099 petal_length 9.4294 4.737 1.990 0.047 0.145 18.714 petal_width 18.2861 9.743 1.877 0.061 -0.809 37.381 ================================================================================ Possibly complete quasi-separation: A fraction 0.60 of observations can be perfectly predicted. This might indicate that there is complete quasi-separation. In this case some parameters will not be identified.
Python
복사
예측값(0,1)은 임곗값 0.5로 설정하여 구해보면
y_pred = result.predict(df)>=0.5 # 0.5이상이면 1, 밑이면 0 # 오차행렬을 구해보면 from sklearn.metrics import confusion_matrix confusion_matrix(df.species,y_pred) array([[49, 1], [ 1, 49]]) # 나머지 분류성능 지표를 확인해보면 from sklearn.metrics import classification_report print(classification_report(df.species,y_pred)) precision recall f1-score support 0 0.98 0.98 0.98 50 1 0.98 0.98 0.98 50 accuracy 0.98 100 macro avg 0.98 0.98 0.98 100 weighted avg 0.98 0.98 0.98 100 # 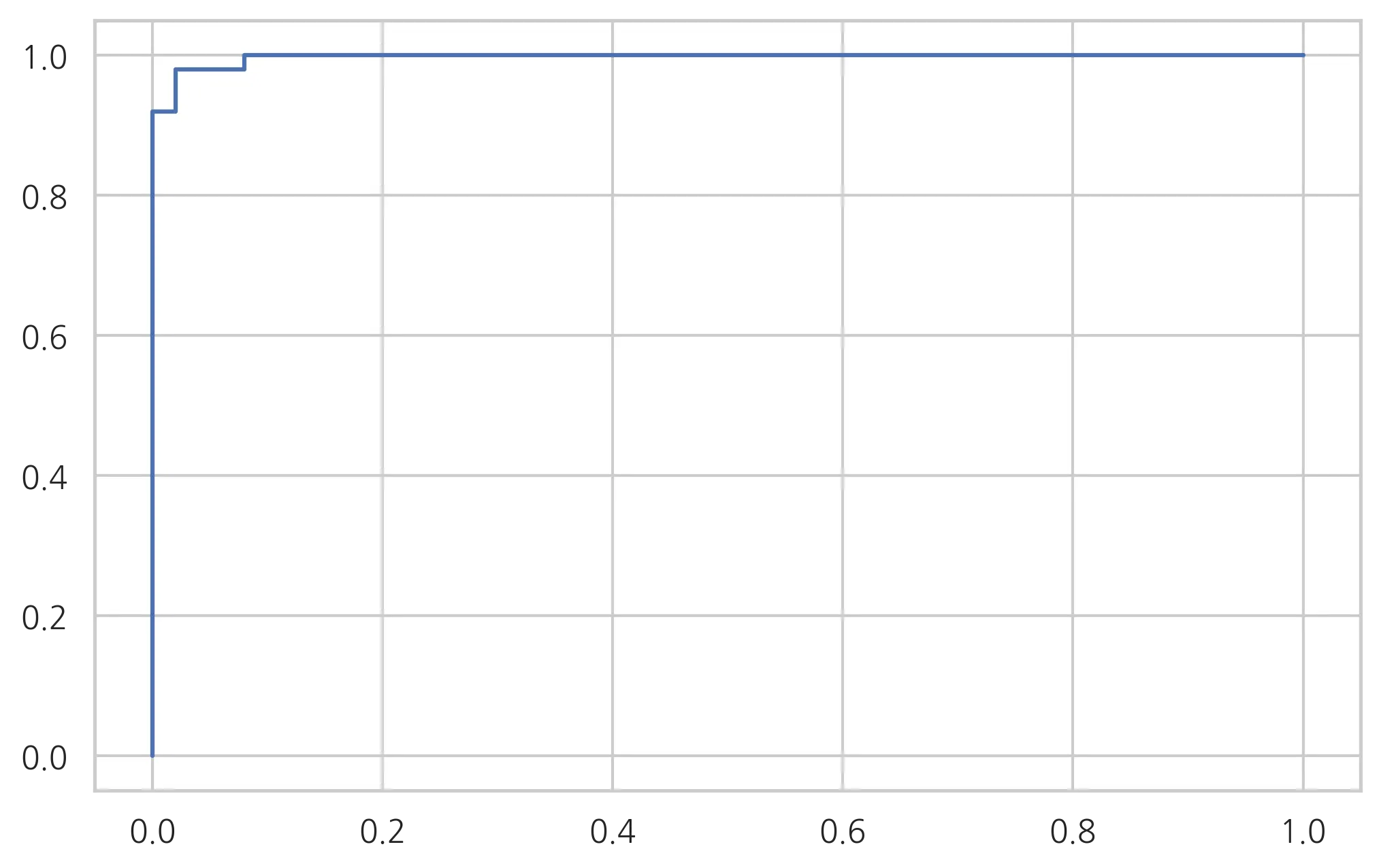roc curve from sklearn.metrics import roc_curve fpr, tpr, thresholds = roc_curve(df.species, result.predict(df)) plt.plot(fpr,tpr) plt.show() # auc from sklearn.metrics import auc auc(fpr,tpr) 0.9972000000000001
Python
복사

미국 의대생의 입학관련 데이터에서의 로지스틱활용

•
Acceptance: 0이면 불합격, 1이면 합격
•
BCPM: Bio/Chem/Physics/Math 과목의 학점 평균
•
GPA: 전체과목 학점 평균
•
VR: MCAT Verbal reasoning 과목 점수
•
PS: MCAT Physical sciences 과목 점수
•
WS: MCAT Writing sample 과목 점수
•
BS: MCAT Biological sciences 과목 점수
•
MCAT: MCAT 총점
•
Apps: 의대 지원 횟수
먼저, 데이터를 가져온다.
data_med = sm.datasets.getrdataset('MedGPA', package='Stat2Data') df_med = data_med.data df_med.tail()
Python
복사
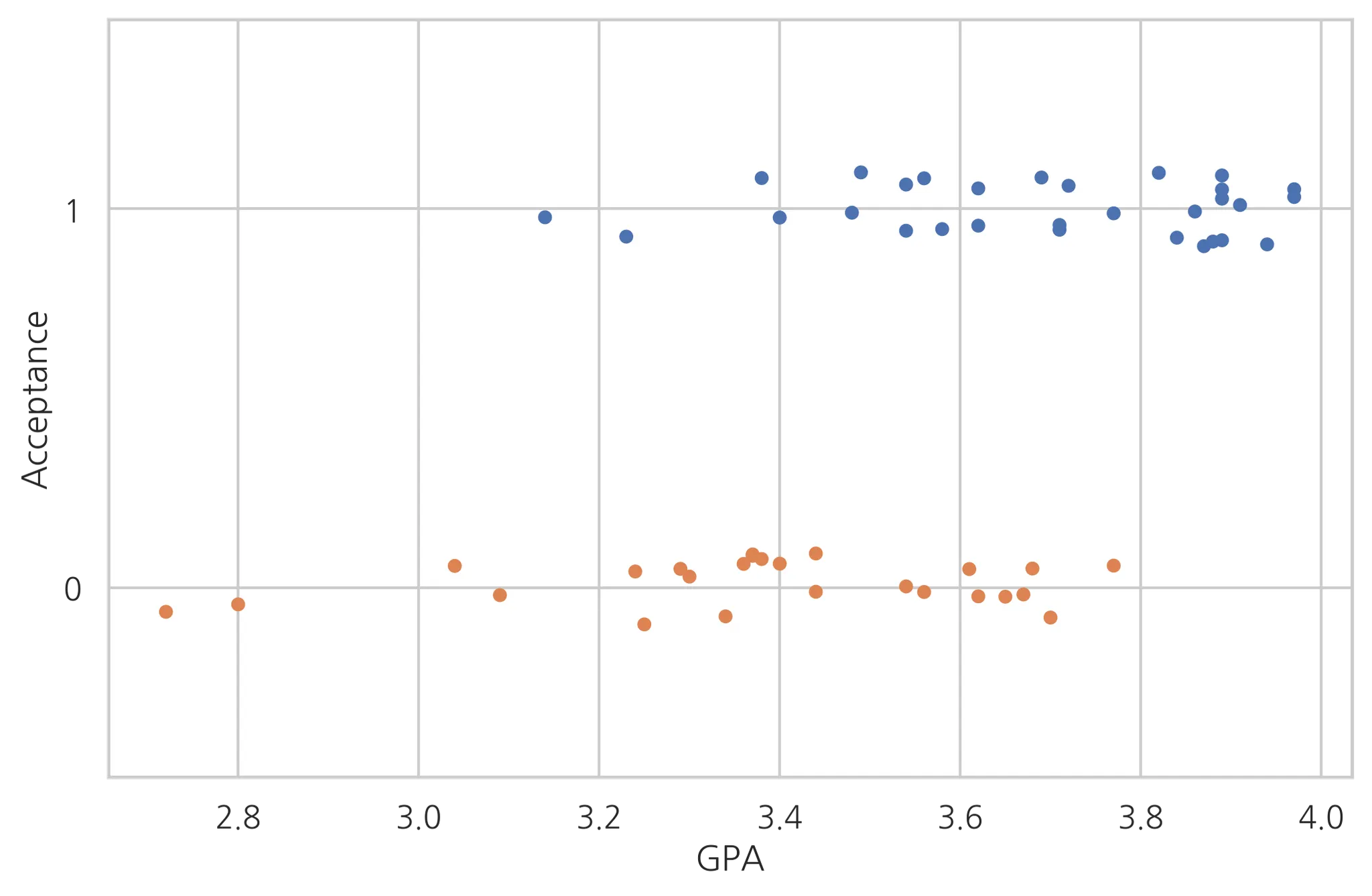
먼저, y(acceptance)와 피처들간의 관계를 살펴보는 것이 좋다. 가장 연관성이 높을 것이라고 예측되는 GPA와의 관계를 살펴보자.
import seaborn as sns sns.stripplot(x='GPA', y='Acceptance', data=df_med, jitter=True, orient='h', order=[1,0]) plt.grid(True) plt.show()
Python
복사
GPA의 값 3.1부터는 GPA가 Acceptance에 영향을 준다고 보기 어렵다. 즉, 어느 정도의 학점평균 이상만 되면 평균학점은 입학여부에 큰 영향을 준다고 보기 힘들다.
이제, 전처리를 해보자. 먼저 MCAT는 나머지 MCAT 과목 점수를 합친 것이므로 종속적이다. 따라서 이 변수는 제거하도록 한다.
마찬가지로 StatsModel의 Logit함수를 사용해서 로지스틱 회귀모델을 적용해보자.
model_med = sm.Logit.from_formula('Acceptance ~ Sex + BCPM + GPA + VR + PS + WS + BS + Apps',df_med) result_med = model_med.fit() print(result_med.summary()) Optimization terminated successfully. Current function value: 0.280736 Iterations 9 Logit Regression Results ============================================================================== Dep. Variable: Acceptance No. Observations: 54 Model: Logit Df Residuals: 45 Method: MLE Df Model: 8 Date: Sat, 06 Jun 2020 Pseudo R-squ.: 0.5913 Time: 10:01:33 Log-Likelihood: -15.160 converged: True LL-Null: -37.096 Covariance Type: nonrobust LLR p-value: 6.014e-07 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -46.6414 15.600 -2.990 0.003 -77.216 -16.067 Sex[T.M] -2.2835 1.429 -1.597 0.110 -5.085 0.518 BCPM -6.1633 6.963 -0.885 0.376 -19.811 7.484 GPA 12.3973 8.611 1.440 0.150 -4.479 29.274 VR 0.0790 0.311 0.254 0.799 -0.530 0.688 PS 1.1673 0.539 2.164 0.030 0.110 2.225 WS -0.7784 0.396 -1.968 0.049 -1.554 -0.003 BS 1.9184 0.682 2.814 0.005 0.582 3.255 Apps 0.0512 0.147 0.348 0.728 -0.237 0.340 ==============================================================================
Python
복사
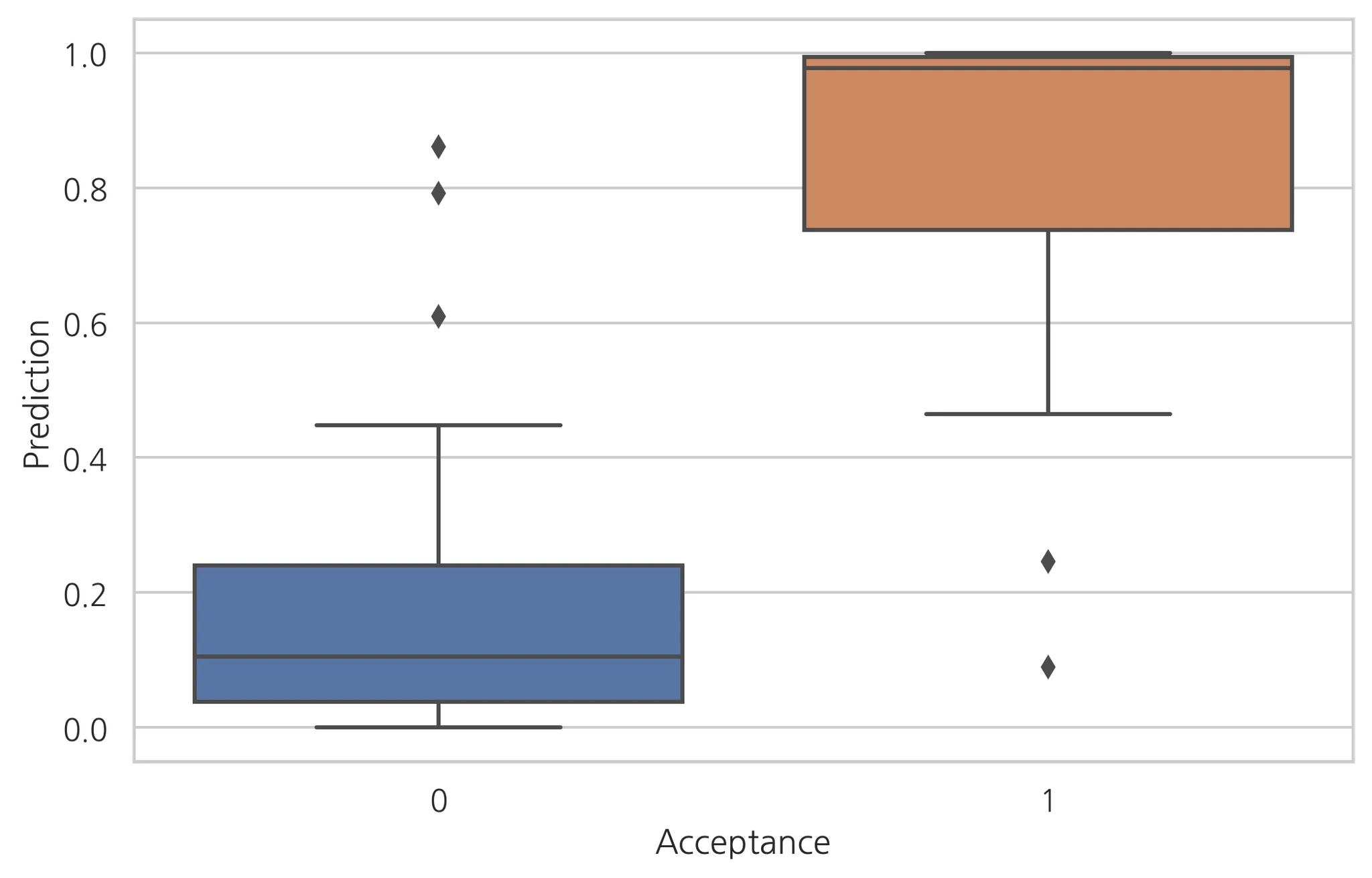
예측결과와 실제값을 비교해보자.
df_med['Prediction'] = result_med.predict(df_med) sns.boxplot(x='Acceptance', y='Prediction') plt.show()
Python
복사
어느정도 예측이 잘 들어맞어 보인다. 이상값들이 실제값과 차이가 나기 때문에 잘 분류하지 못한 경우라고 볼 수 있다.
이제, 유의하지 않은 변수들을 제거해서 좀 더 정확도를 높여보자. 유의확률이 높아보이는 ps와 bs만을 가지고 다시 로지스틱 회귀분석을 진행한다.
model_med = sm.Logit.from_formula('Acceptance~PS+BS', df_med) result_med = model_med.fit() print(result_med.summary()) Optimization terminated successfully. Current function value: 0.460609 Iterations 7 Logit Regression Results ============================================================================== Dep. Variable: Acceptance No. Observations: 55 Model: Logit Df Residuals: 52 Method: MLE Df Model: 2 Date: Sat, 06 Jun 2020 Pseudo R-squ.: 0.3315 Time: 10:01:36 Log-Likelihood: -25.333 converged: True LL-Null: -37.896 Covariance Type: nonrobust LLR p-value: 3.503e-06 ============================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -15.5427 4.684 -3.318 0.001 -24.723 -6.362 PS 0.4798 0.316 1.518 0.129 -0.140 1.099 BS 1.1464 0.387 2.959 0.003 0.387 1.906 ==============================================================================
Python
복사
0.4798PS + 1.1464BS 의 점수가 15.5427 + 0.5보다 크면 합격이라고 예측할 수 있다.

LogisticRegression패키지를 활용한 로지스틱 회귀 분석

사이킷런에서 제공하는 LogisticRegression 모델을 사용해서 로지스틱 회귀 분석을 진행해보자.
실습할 데이터는 개인대출 데이터다.
•
Experience 경력
•
Income 수입
•
Famliy 가족단위
•
CCAvg 월 카드사용량
•
Education 교육수준 (1: undergrad; 2, Graduate; 3; Advance )
•
Mortgage 가계대출
•
Securities account 유가증권계좌유무
•
CD account 양도예금증서 계좌 유무
•
Online 온라인계좌유무
•
CreidtCard 신용카드유무
•
Personal Loan (0 과 1의 값을 갖는 레이블 변수)
# 필요한 라이브러리 로드 import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score, roc_auc_score, roc_curve, classification_report, auc import statsmodels.api as sm import matplotlib.pyplot as plt ploan = pd.read_csv('./Personal Loan.csv') # 사용하지 않을 변수 제거 (ID, Zip code) ploan_processed = ploan.dropna().drop['ID','ZIP code'], axis=1, inplace=False) # b0 를 위한 상수항 추가 ploan_processed = sm.add_constant(ploan_processed.has_constant='add') ploan_processed.head()
Python
복사
피처 데이터와 레이블 데이터를 분리하고 학습데이터와 평가 데이터를 분리하자.
# 대출을 하면 1, 안했을 때 0이다. feature_columns = ploan_processed.columns.difference(['Personal Loan']) # y열만 제거한 열들 X = ploan_processed[feature_columns] y = ploan_processed['Personal Loan'] # 학습/테스트 데이터 분리 train_X, test_X, train_y, test_y = train_test_split(X,y,stratify=y,test_size=0.3,random_state=0) print(train_X.shape, test_X.shape, train_y.shape, test_y.shape)
Python
복사
비교를 위해 sm.Logit으로 먼저 예측모델을 만들어보자.
model = sm.Logit(train_y,train_X) result = model.fit() result.summary() result.params # 각 설명변수들의 회귀계수값들을 확인할 수 있다.(log취해진) np.exp(result.params) # 이제 실제 회귀계수값들이다. # 테스트데이터로 예측해보자 pred_y = result.predict(test_X) pred_y
Python
복사
이 값들은 1이 될 확률을 나타낸 값이 된다. 임곗값을 설정해서 분류해주는 함수 cut_off를 만들어보자.
def cut_off(y, threshold): Y = y.copy() # 기존 y값에 영향 없도록 복사한 값 사용한다. Y[Y>threshold] = 1 Y[Y<threshold] = 0 return Y.astype(int) # 기본적인 임곗값 0.5 로 설정 pred_Y = cut_off(pred_y, 0.5) # 이제, 예측확률값을 기반으로한 y에 0과 1을 부여해줬다. pred_Y
Python
복사
임곗값을 더 높이면 불량품(1) 을 더 잘 선별할 수 있다. 그때그때 상황에 맞게 조절한다. 이제 모델 성능 지표를 확인해보자.
# 오차행렬 cfmat = confusion_matrix(test_y,pred_Y) print(cfmat)
Python
복사
정확도(예측한 것들 중 옳게 예측한 것들의 비율)를 계산해보자.
def acc(cfmat): return (cfmat[0,0]+cfmat[1,1])/(cfmat[0,1]+cfmat[0,0]+cfmat[1,0]+cfmat[1,1]) acc(cfmat)
Python
복사
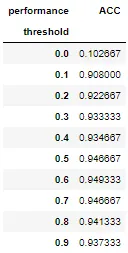
이번에는 임곗값을 변화시켜가면서 정확도를 확인해보자.
threshold = np.arrange(0,1,0.1) table = pd.DataFrame(columns=['ACC']) # 각 임곗값에 따른 정확도를 표현할 데이터프레임 형성 for i in threshold: pred_Y = cut_off(pred_y,i) cfmat = confusion_matrix(test_y,pred_Y) table.loc[i] = acc(cfmat) table.index.name = 'threshold' table.columns.name = 'performance' table
Python
복사
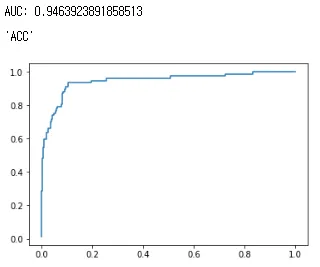
# roc fpr, tpr, thresholds = roc_curve(test_y,pred_y) plt.plot(fpr,tpr) # auc auc(fpr, tpr) # 0.9463...
Python
복사

비용함수

결론적으로 로지스틱 회귀는 비용 함수로 크로스 엔트로피 함수를 사용하며, 가중치를 찾기 위해서 크로스 엔트로피 함수의 평균을 취한 함수를 사용합니다.

최적화함수

위의 크로스 엔트로피 함수를 최소화할 옵티마이저로 어떤 옵티마이저를 사용해야 할까?
•
그냥 경사하강법

주요 하이퍼파라미터

from sklearn.linear_model import LinearRegression LinearRegression(penalty='l2', tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='lbfgs', max_iter=100, multi_class='auto',verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
Python
복사
•
penalty: 과적합을 줄이기 위한 규제방식
◦
‘l2’(default) , ‘l1’ , ‘elasticnet’ , None
◦
solver 매개변수의 가능한 조합을 고려해야함
•
tol : 0.0001(default)
•
C : 규제강도(기본값 1) : 값이 작을수록 규제 강함. 음수값 x,
•
fit_intercept(default=True) : 모델을 생성할 때 상수값 포함시키는지 여부
•
Intercept_scaling(default=1) : solver가 ‘liblinear’ 이고 fit_intercept가 True 일 경우에만 유용하다.
•
class_weight(default=None) : {class_label : weight} 또는 ‘balanced’ 또는 None
•
solver : 모델의 최적화 문제에 사용되는 알고리즘
◦
‘lbfgs’(default)
◦
‘liblinear’
◦
‘newton-cg’
◦
‘newton-cholesky’
◦
‘sag’
◦
‘saga’
→ solver 는 다음과 같은 조건을 고려해서 결정한다.
1) 작은 데이터 셋에는, ‘liblinear’이 좋다. 큰 데이터 셋에는 ‘sag’ 또는 ‘saga’가 빠르다.
2) 다중클래스 문제에는, ‘newton-cg’, ‘sag’, ‘saga’, ‘lbfgs’ 만이 사용가능하다.
3) ‘liblinear’는 ovr(one-versus-rest) 에 한정되어서 사용된다.
4) ‘newton-cholesky’는 데이터셋이 피처수에 비해 매우 클때 아주 좋은 선택이 되고, 특히 범주형 변수의 원핫인코딩에서 범주가 많지 않을 때 더욱 좋다. 이 알고리즘은 이진분류와 ovr 다중 분류에만 사용된다.
•
max_iter(기본값 100): 경사하강법 반복횟수